Odcinek o długości a∛2 można skonstruować poprzez narysowanie w układzie współrzędnych dwóch wykresów paraboli. Pierwsza o wzorze: y=x2 (czyli taka "z nogami do góry") powinna przeciąć drugą o wzorze: x=1/2y2 (czyli taką "z nogami w prawo") w dwóch punktach:
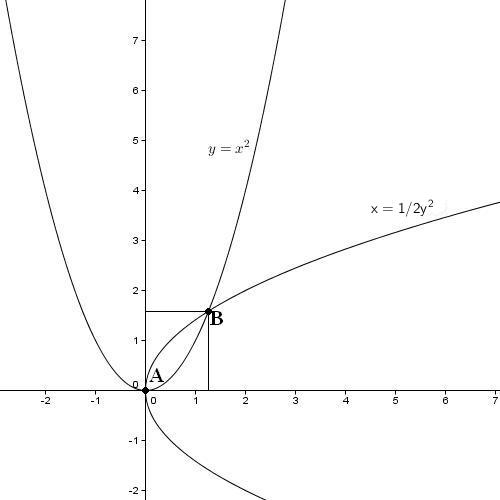
Punkt A ma współrzędne A=(0;0). Współrzędne punktu B można obliczyć podstawiając y z pierwszego równania do drugiego. Będzie to:
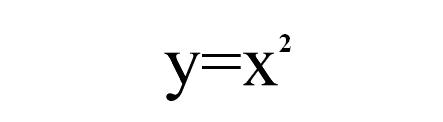
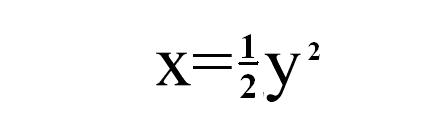
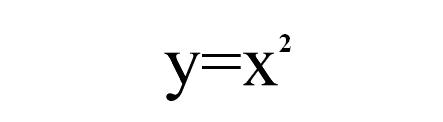
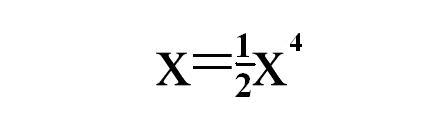

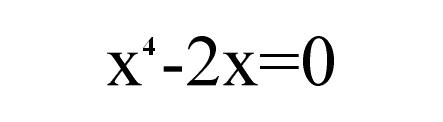
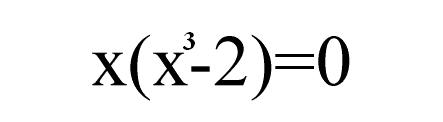
Rozwiązując dalej otrzymujemy następujące rozwiązania:
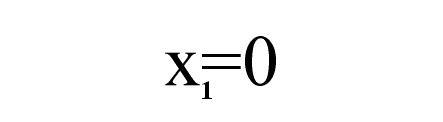
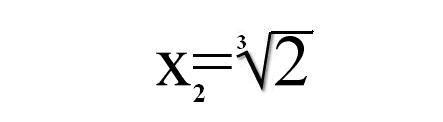
Zatem odległość punktu B od osi OY wynosi ∛2. Problem podwojenia sześcianu jest rozwiązany. Przyrząd do kreślenia paraboli można swobodnie zbudować za pomocą linijki, ekierki i sznurka. Starożytni jednak nie mieli zaufania do krzywych takich jak parabola, czyli w każdym punkcie innych. Postanowili znaleźć inne rozwiązanie - MEZOLABIUM .