Problem podwojenia sześcianu, znany też pod nazwą problemu delijskiego, to jeden z trzech, obok trysekcji kąta i kwadratury koła, wielkich problemów starożytnej matematyki greckiej, polegający na zbudowaniu sześcianu o dwukrotnie większej objętości od początkowego. Nazwa "problem delijski" pochodzi od wyspy Delos, gdzie według legendy przedstawionej poniżej, miał wystąpić on po raz pierwszy.
Według starej legendy, pewnego dnia Ateny nawiedziła zaraza. Lud wysłał więc posłańca do wyroczni Apollina w Delos, aby ten dowiedział się, jak zaradzić w tej sprawie. Odpowiedź wyroczni mówiła, że aby zaraza ustąpiła, należy zbudować Apollinowi dwukrotnie większy ołtarz, niż ten dotychczasowy.
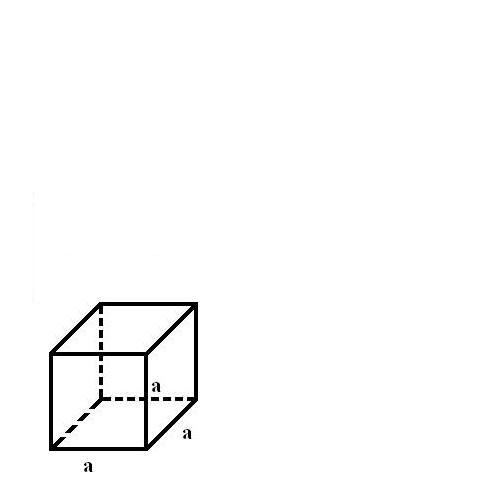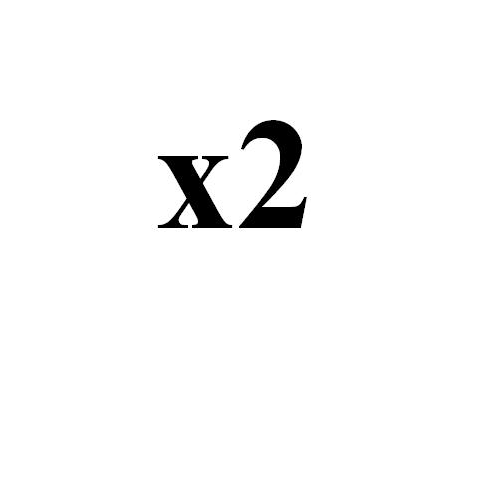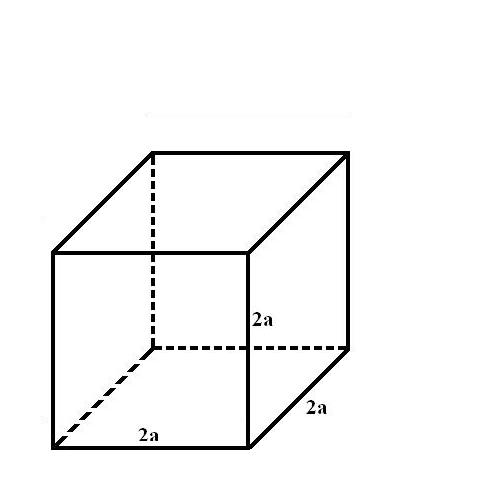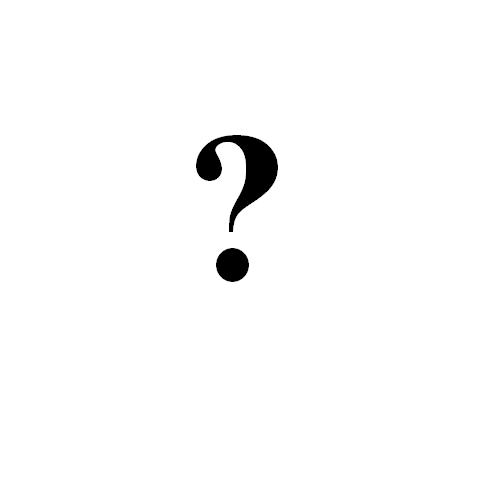
Ateńczycy zrozumieli polecenie zbyt dosłownie. Ponieważ ołtarz miał kształt sześcianu, każdą z krawędzi powiększyli dwukrotnie. Zaraza jednak nie ustąpiła. Wysłano więc ponownie posłańca, któremu wyrocznia wytłumaczyła, że objętość ołtarza była osiem razy większa od poprzedniego.
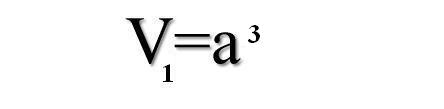
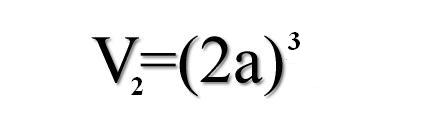
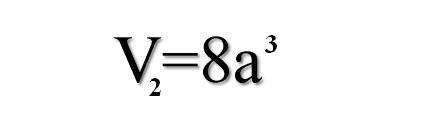
Lud postanowił zwórcić się do Platona, który rzekł: "Jeśli Apollon domaga się tej konstrukcji ustami wyroczni, to przecież nie dlatego, że potrzebuje podwójnego ołtarza. To dlatego, że ma za złe Grekom lekceważenie matematyki i ich niechęć do geometrii".
W końcu Grecy doszli do wniosku, że skoro ołtarz był z litego brązu (kupowanego na wagę), to dwukrotnie większy oznacza o dwukrotnie większej objętości. I tak powstał problem podwojenia sześcianu.
Zadanie zostało zlecone największym matematykom ówczesnych czasów. Dlaczego?