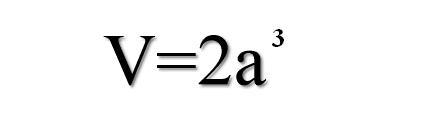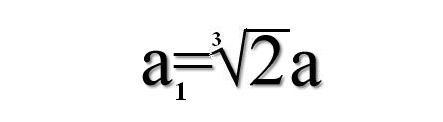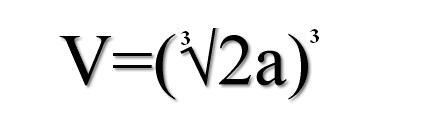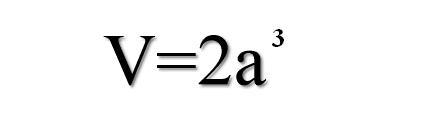W końcu zrozumiano, że aby sześcian miał dwukrotnie większą objętość od danego sześcianu o boku długości a, z danego równania należy wyliczyć długość boku a:
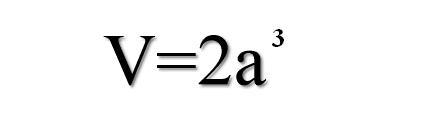
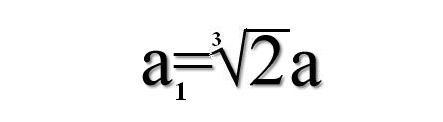Podwojenie sześcianu jest to w takim razie poszukiwanie odcinka o długości a∛2, gdzie a jest długością odcinka danego.
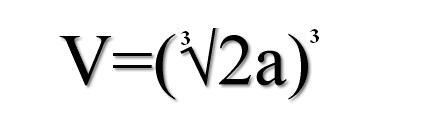
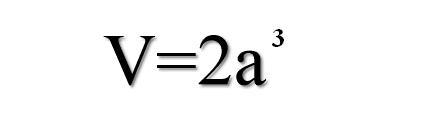
Stąd wynika, że podwojona objętość sześcianu o boku a jest równa objętości sześcianu o boku a∛2:
Znów pojawił się problem. Nie dało się skonstruować takiego odcinka za pomacą cyrkla i linijki. Współcześnie zostało to udowodnione za pomocą twierdzenia. Taki odcinek można jednak łatwo skonstruować, gdy umie się kreślić parabole. I to pierwsze możliwe rozwiązanie problemu. Inne rozwiązania są możliwe dzięki mezolabium skonstruowanym przez Erastotenesa z Cyreny oraz konchoidzie Nikomedesa. W dalszej części zostaną omówione dwa pierwsze sposoby. A więc do działa!
PARABOLE
MEZOLABIUM