Wszystkie możliwości na jednym wykresie:
Okrąg, elipsa, parabola, hiperbola z wszystkimi możliwymi ekscentrycznościami od zera do nieskończoności. Poniżej znajduje się równanie krzywej przedstawiające wszystkie możliwości orbit:
(1)
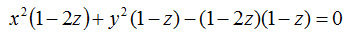
Okazuje się, że można to równanie przedstawić za pomocą dwóch funkcji. Przyjmuje ono postać:
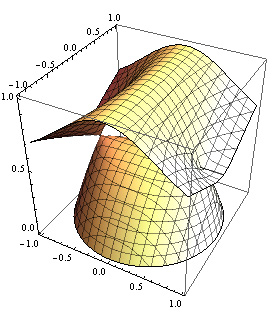
(Obraz wygenerowany z wtyczki WolframAlpha.)
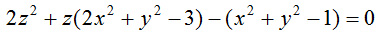
Gdzie dziedziną jest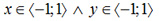 
, a zbiorem wartości 
.
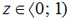Z czego możemy obliczyć deltę:
(3)
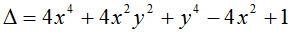
A następnie przy założeniu delty większej od zera (co zapewnia nam dziedzina) otrzymujemy dwa rozwiązania:
(4)
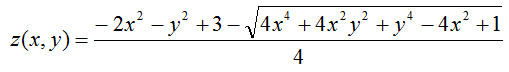
lub:
(5)
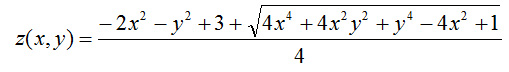
Patrząc na wykres rzeczywiście widzimy dwie powierzchnie, górną i dolną, funkcja (5) przedstawia część górną wykresu, natomiast funkcja (4) przedstawia część dolną. Ciekawy jest fakt, iż równoległy do podstawy przekrój wykresu jest daną orbitą. Tak zatem wykres ten zestawią wszystkie możliwości orbit.
Ekscentryczność:
Wyróżniamy typy orbit w zależności od ekscentryczności:
- Jeżeli ekscentryczność wynosi zero jest to orbita kołowa (okrąg),
- Jeżeli ekscentryczność jest większa od zera i mniejsza od 1 to jest to orbita eliptyczna (elipsa),
- Jeżeli ekscentryczność jest równa 1 to jest to orbita paraboliczna (parabola),
- Jeżeli ekscentryczność jest większa od 1 to jest to orbita hiperboliczna (hiperbola),
| Typ | Równianie | Ekscentryczność |
| Okrąg |  |  |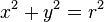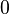
| Elipsa |  |  |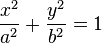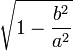
| Parabola |  |  |
| Hiperbola |  |  |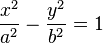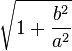
Gdzie: a - to półoś wielka, b- to półoś mała.
Ze wzoru (1) i wzoru na elipsę(również okrąg) oraz wzoru na hiperbolę (także na parabolę) możemy dopatrzeć się związków:
(6)
i
(7)
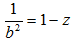
Zatem:
(8)
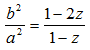
Znamy więc także wzór na ekscentryczność w zależności od parametru z. Wystarczy za stosunek we wzorach w tabelce podstawić stosunek (8).
Animacje ilustrujące:
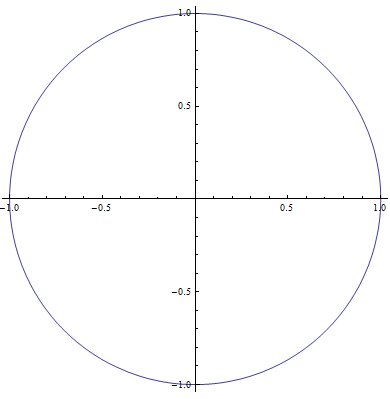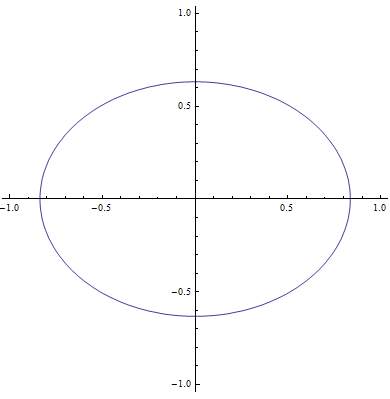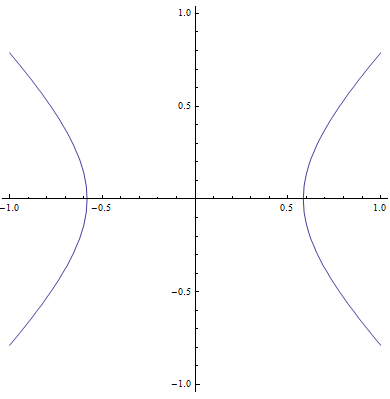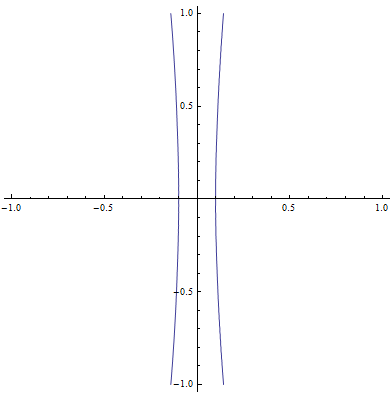
Poniższa animacja przedstawia różne orbity i ich ekscentryczności.
