Fraktale
Rys historyczny
Pojęcie fraktala zostało wprowadzone do matematyki przez francuskiego informatyka i matematyka polskiego pochodzenia Benoîta Mandelbrota w latach siedemdziesiątych XX wieku. Odkryty przez niego zbiór Mandelbrota nie był jednak pierwszym przykładem fraktala. Wcześniej istniała już cała gama zbiorów postrzeganych jednak głównie jako kontrprzykłady pewnych twierdzeń. Szczególnymi fraktalami – nie nazywając ich po imieniu – zajmowali się Georg Cantor, Giuseppe Peano, Wacław Sierpiński, Paul Lévy, a także Donald Knuth. Szczególny wkład w rozwój geometrycznej teorii miary wniósł Abraham Bezikowicz, który skonstruował również wiele konkretnych fraktali o paradoksalnych własnościach. Również zbiór Julii, ściśle związany ze zbiorem Mandelbrota, był badany w latach 20. zeszłego wieku. Mandelbrot używając komputera do wizualizacji uczynił z fraktali przedmiot intensywnych badań. O ważności tego zagadnienia zadecydowały zastosowania w różnych dziedzinach, zwłaszcza poza matematyką, np. obecnie prawie każdy telefon komórkowy korzysta z wbudowanej anteny fraktalnej. Liczne odpowiedniki fraktali istnieją też w naturze.
Właściwości
Za jedną z cech charakterystycznych fraktala jest samopodobieństwo, to znaczy podobieństwo fraktala do jego części. Co więcej, zbiory fraktalne mogą być samoafiniczne, to znaczy, że część zbioru może być obrazem całości przez pewne przekształcenie afiniczne. Dla figur samopodobnych można określić wielkość zwaną wymiarem samopodobieństwa lub wymiarem pudełkowym. Drugą ważną cechą fraktali jest nieskończona subtelność - nie da się ich tak powiększyć, by uzyskać ciągłe kształty (odcinki, okręgi, itp).
Fraktale są w większości generowane komputerowo, przy użyciu skomplikowanych algorytmów wykorzystujących zbiory przekształceń afinicznych lub liczących zbieżność ciągów z parametrem dla każdego piksela obrazu. Istnieją także struktury, które można stworzyć w domowym zaciszu przy użyciu ołówka i linijki.
Przykłady fraktali
Zbiór Cantora
Jest jednym z najprostszych fraktali.

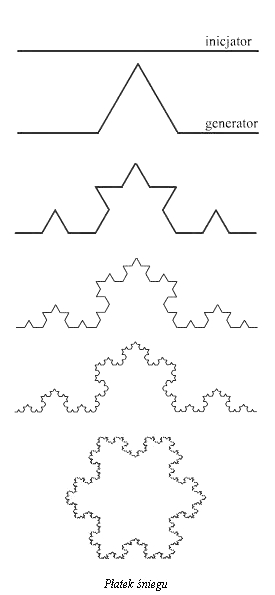
Krzywa Kocha
Kolejny prosty fraktal. Wygląd podobny do płatka śniegu nie jest tu przypadkowy.
Paproć Barnsleya
W naturze możemy znaleźć wiele organizmów, których struktura przypomina fraktal.

Jest określona wzorem

gdzie a jest pewną liczbą z przedziału (0,1) natomiast b
jest liczbą nieparzystą, spełniającą warunek ab>1+3π/2.
Zbiór Mandelbrota
Zwany także żukiem Mandelbrota. Jego brzeg jest jednym ze sławniejszych fraktali.

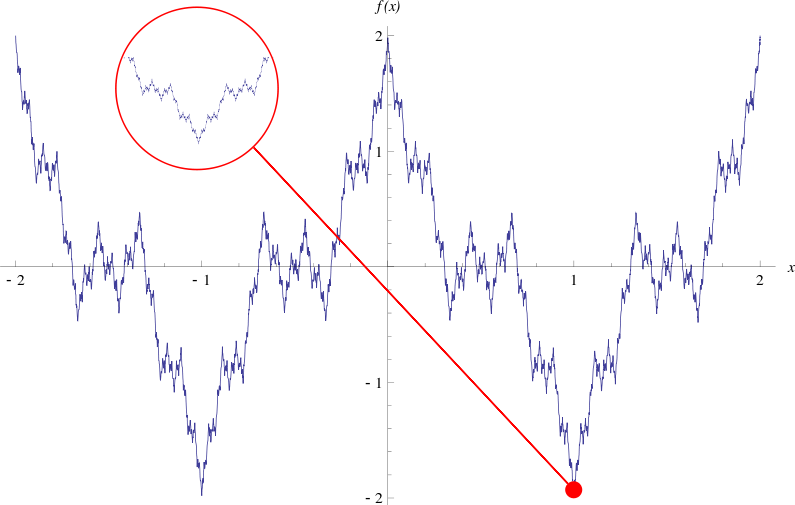
Funkcja Weierstrassa
Płonący statek
Opisany przez Michaela Michelitscha i Otto E. Rösslera w 1992.

Fraktale różnego pochodzenia




Przykłady struktur fraktalnych w naturze
Kalafior Brassica oleracea
Roślina występująca we Włoszech.

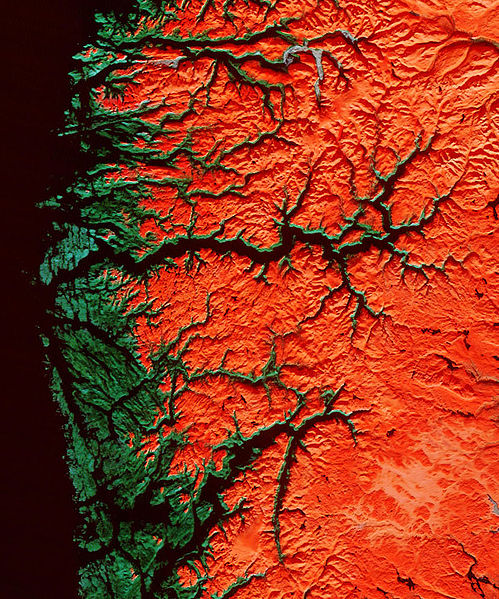
Fiordy
Zdjęcie satelitarne fiordów Sognefjorden i Hardangerfjorden w Norwegii.
Chmury

Galaktyki

Drzewa

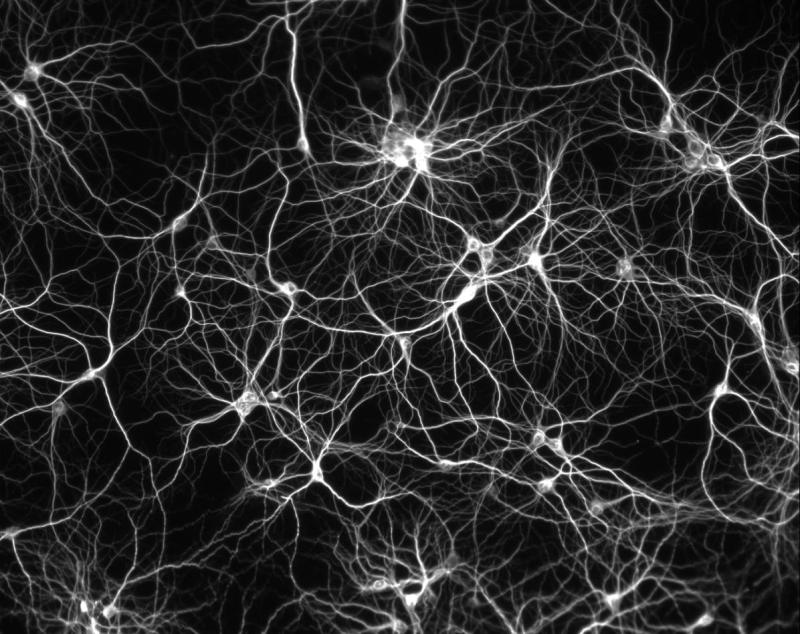
Sieć neuronów w mózgu
Pioruny
