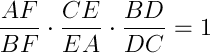
Twiedzenie Cevy:
Jeżeli proste AD, BE, CF przechodzą przez wierzchołki trójkąta ABC i przecinają się w jednym punkcie lub są równoległe i przecinają boki AB, BC i CA lub ich przedłużenia odpowiednio w punktach D, E i F to:
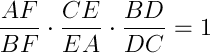
Dowód:
Na potrzeby dowodu należy rozpatrzyć dwa przypadki: proste AD, BE, CF przecinają się w jednym punkcie i proste AD, BE, CF są równoległe.
1. Proste AD, BE, CF przecinają się w jednym punkcie
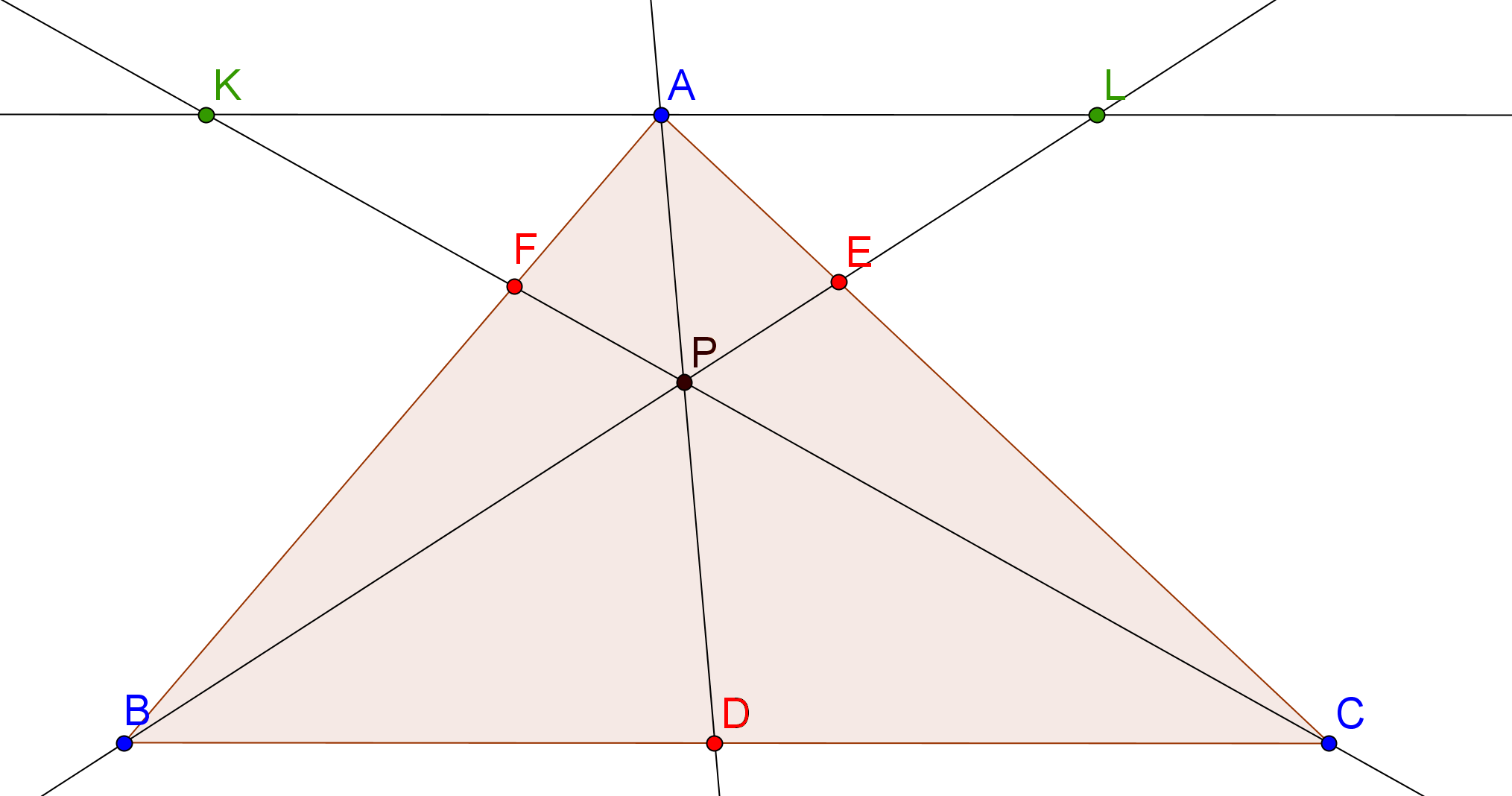
Do przeprowadzenia dowodu dorysujmy prostą KL przechodzącą przez A, taką, że:
Wtedy na podstawie cechy podobieństwa ![]() kąt-kąt-kąt otrzymujemy:
kąt-kąt-kąt otrzymujemy:
więc:
.gif)
(1)
oraz:
więc:
.gif)
(2)
oraz:
więc:
.gif)
(3)
oraz:
więc:
.gif)
(4)
Po porównaniu równości (3) i (4) otrzymujemy:
.gif)
Powyższy zapis równoważny jest:
.gif)
(5)
Dzięki wymnożeniu stronami (1), (2), (5) otrzymujemy:
.gif)
Co po skróceniu:
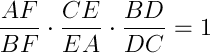
2. Proste BD, EA, CF są równoległe.
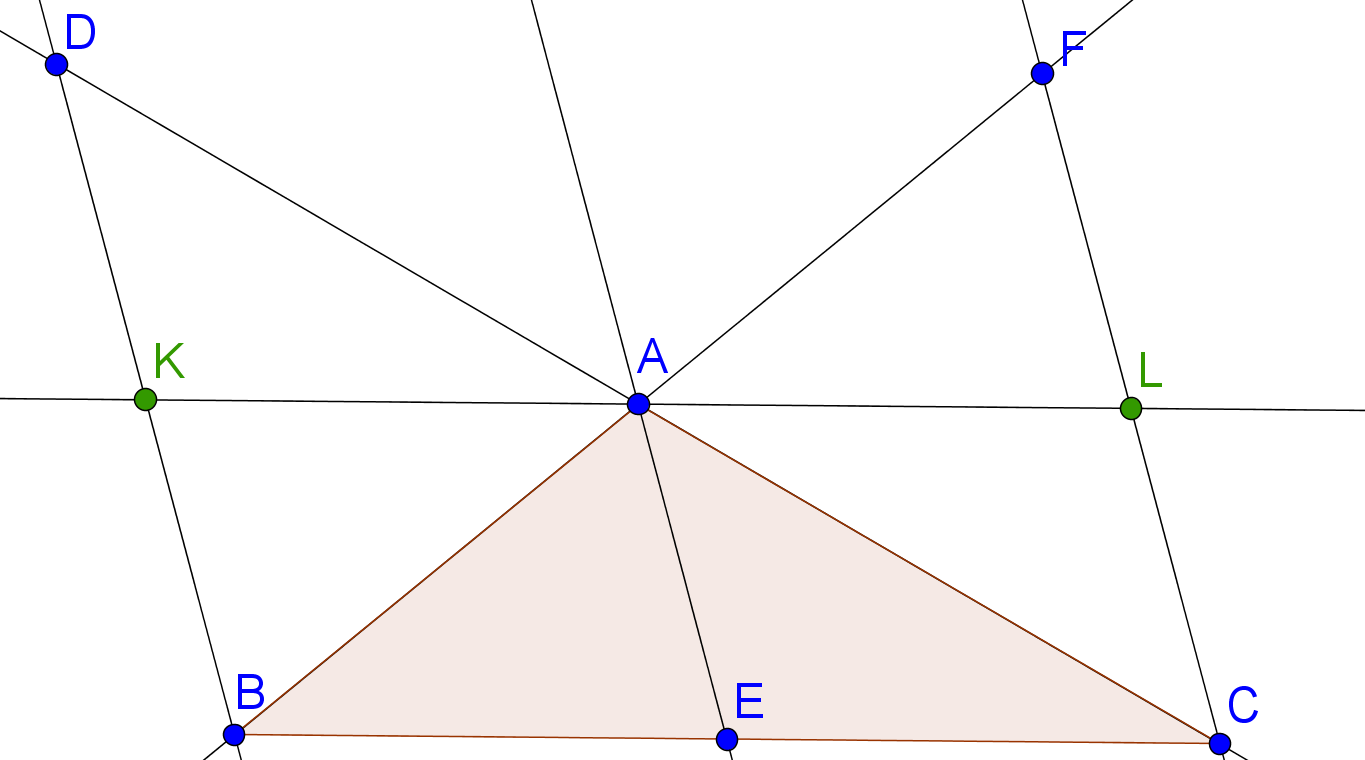
Na potrzeby dowody dorysujemy prostą KL przechodzącą przez A, taką że:
Na podstawie cechy podobienstwa ![]() kat-kąt-kąt:
kat-kąt-kąt:
więc:
.gif)
(6)
oraz:
więc:
.gif)
(7)
Po przekształceniu powyższych równości otrzymujemy:
.gif)
i
.gif)
Co pozwala nam zapisać:
.gif)
Po odpowiednich przekształceniach otrzymujemy:
.gif)
Z rysunku wynika także:
.gif)
(8)
a po przekształceniu:
.gif)
(9)
Po wymnożeniu stronami otrzymujemy:
.gif)
Co po skróceniu:
.gif)
Powyższy zapis jest równoważny:
.gif)
Tak więc wykazaliśmy słuszność Twierdzenia Cevy.
* Taką formę dowodu zaproponował S. I. Zetel w Geometrii trójkąta PZWS Warszawa 1964