Punkt Nagela - dowód

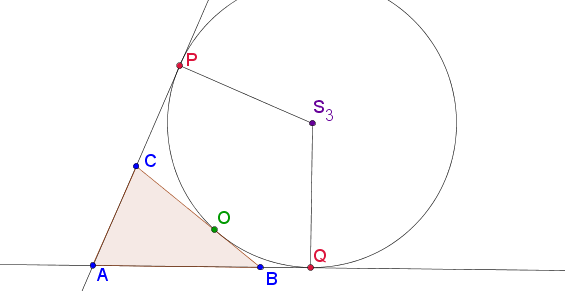
Na potrzeby dowodu rozważać będziemy okrąg o środku S₃ dopisany do boku BC. Niech:

O - będzie punktem styczności z bokiem BC,
Q – punktem styczności z przedłużeniem boku AB,
P – punktem styczności z przedłużeniem boku AC.

Z twierdzenia o stycznych do okręgu otrzymujemy:

Oznaczmy obwód trójkąta ABC przez:

gdzie p- połowa obwodu.

Wtedy:

Z powyższego zapisu wynika, że punkt O i wierzchołek A podzieliły obwód trójkąta ABC na połowę. Po przeprowadzeniu identycznych rozważań dla pozostałych okręgów dopisanych dochodzimy do analogicznych wniosków. Punkty styczności z przeciwległymi wierzchołkami dzielą obwód na połowy. Dzięki temu można stwierdzić, że:

a także:

Przyjmując powyższe równości można zapisać:

oraz:

więc:

Co pozwala na podstawie twierdzenia Cevy stwierdzić, że proste AO, BN i CM przecinają się w jednym punkcie, zwanym punktem Nagela. Na rysunku oznaczony K.

* Taką formę dowodu zaproponował S. I. Zetel w Geometrii trójkąta PZWS Warszawa 1964