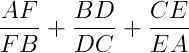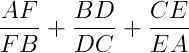W tej części pracy zamieściłem kilka zadań znalezionych w sieci opierających się na treściach przybliżonych wcześniej. Zadania mają zróżnicowany poziom trudności.
Życzę powodzenia!
- *Wykaż, że w trójkącie prostokątnym iloczyn promieni okręgów dopisanych
do przyprostokątnych jest równy polu trójkąta.
- *Wykaż, że odległość wierzchołka A trójkąta ABC od punktu styczności T
okręgu dopisanego jest równa połowie obwodu.
- *Czy jeśli w trójkącie ABC środki okręgów dopisanych, stycznych do każdego7nbspz boków AB, AC, BC połączymy
odpowiednio z wierzchołkami C, B, A to otrzymane proste przetną się w jednym punkcie? Odpowiedź uzasadnij.
- *Czy jeśli7nbspw trójkącie ABC środek okręgu dopisanego, stycznego do boku AB połączymy z wierzchołkiem C
to otrzymany odcinek będzie leżał na dwusiecznej kąta ACB? Odpowiedź uzasadnij.
- **Wyznacz najmniejszą wartość wyrażenia:
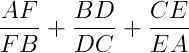 Kiedy jest ona osiągana?
Kiedy jest ona osiągana?
- **Punkty D, E, F są punktami styczności okręgu wpisanego w trójkąt ABC odpowiednio do boków BC, CA, AB. Wykaż, że proste AD, CA, AB przecinają się w jednym punkcie (tzw. punkcie Gergonne’a).
- **Punkty D, E, F są punktami styczności okręgów dopisanych do trójkąta ABC odpowiednio do boków BC, CA, AB. Wykaż, że proste AD, BE, CF przecinają się w jednym punkcie.
- **Okręgi dopisane do trójkąta ABC są styczne do boków BC i AC odpowiednio w punktach D i E. Wykazać, że BD=AE.
- ***Jaki warunek powinny spełniać kąty trójkąta ABC , żeby dwusieczna kąta A, środkowa poprowadzona z wierzchołka B i wysokość poprowadzona z wierzchołka C przecinały się w jednym punkcie? ( XIII OM - III - Zadanie 3)