Z racji tego, że liczby Catalana spełniają poniższą zależnosć:
Widoczne jest, że każda z liczb Catalana jest naturalną.
Zastosowania Kombinatoryczne:
Liczba dróg ▼
Możemy wyrazić n-tą liczbą Catalana ilość wszystkich łamanych "dróg" zaczynajacych się w początku układu
współrzędnych, a kończących się w punkcie (0,2n). Każda z nich złożona jest z pojedynczych odcinków położonych
w I ćwiartce układu o początku (x,y) i końcu (x+1,y+1), albo (x-1,y+1), gdzie x i y są naturalne.
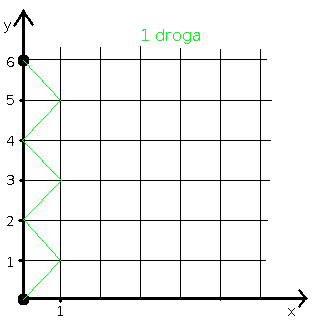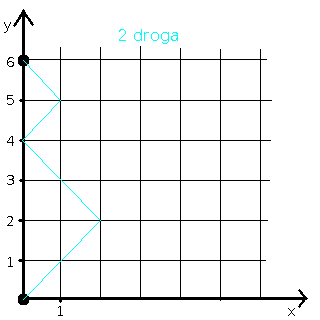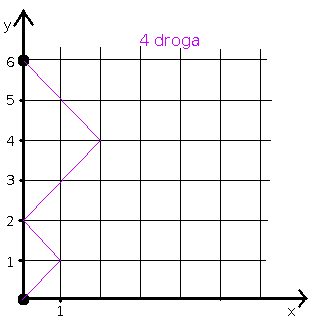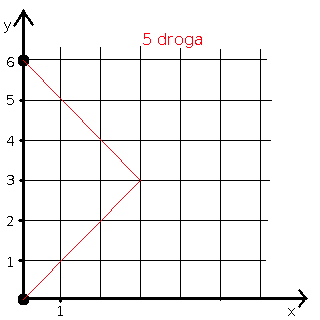
Przykład: policz liczbę możliwych dróg od początku układu współrzędnych do punktu (0,6).
W naszym przykładzie 2n=6, czyli n=3. Liczymy:
Odpowiedź: istnieje 5 takich dróg.
Możemy to potwierdzić rysunkiem:
Przykład: policz liczbę możliwych dróg od początku układu współrzędnych do punktu (0,6).
W naszym przykładzie 2n=6, czyli n=3. Liczymy:
Odpowiedź: istnieje 5 takich dróg.
Możemy to potwierdzić rysunkiem:

Liczba rozmieszczeń nawiasów ▼
Jako znak ★ uznajemy pewne działanie dwuargumentowe. Liczba Cn-1 wyraża liczbę sposobów,
na które można rozmieścić nawiasy w wyrażeniu n-argumentowy.
Przykład: oblicz, na ile sposobów można rozmieścić nawiasy w 3 argumentowym wyrażeniu.
Będziemy musieli policzyć C2.
Odpowiedź: nawiasy możemy ustawić na 2 sposoby. Są to:
a1★(a2★a3) oraz (a1★a2)★a3
Przykład: oblicz, na ile sposobów można rozmieścić nawiasy w 3 argumentowym wyrażeniu.
Będziemy musieli policzyć C2.
Odpowiedź: nawiasy możemy ustawić na 2 sposoby. Są to:
a1★(a2★a3) oraz (a1★a2)★a3
Liczba podziałów na trójkąty ▼
Liczbę sposobów podziału wielokąta wypukłego, która ma n+2 krawędzi na różne trójkąty za pomocą przekątnych
wynosi Cn.
Przykład: oblicz ilość sposobów podziału sześciokąta foremnego na różne trójkąty za pomocą przekątnych.
Sześciokąt foremny jest wielokątem wypukłym, więc możemy policzyć zadanie ze wzoru. Liczymy C4:
Odpowiedź: ilość sposobów podziału sześciokata foremnego na różne trójkąty za pomocą przekątnych wynosi 14.
Przykład: oblicz ilość sposobów podziału sześciokąta foremnego na różne trójkąty za pomocą przekątnych.
Sześciokąt foremny jest wielokątem wypukłym, więc możemy policzyć zadanie ze wzoru. Liczymy C4:
Odpowiedź: ilość sposobów podziału sześciokata foremnego na różne trójkąty za pomocą przekątnych wynosi 14.
Liczba monotonicznych dróg ▼
Mając kwadrat o boku n, możemy za pomocą n-tej liczby Catalana policzyć ilość wszystkich możliwych monotonicznych dróg
rozpoczynających sie z dolnego lewego wierzchołka, prowadzących do górnego prawego, takich, żeby nigdy nie przekraczać
przekatnej, która łączy te wieszchołki.
Przykład: oblicz ilość możliwych monotonicznych dróg w trójkącie równoramiennym o długości ramienia 3 i kącie prostym między ramionami. Droga ma prowadzić z jednego wierzchołka przy przeciwprostokątnej do drugiego takiego wierzchołka.
Rozwiązanie otrzymamy obliczając C3.
Nasz wynik możemy potwierdzić rozrysowując wszystkie przypadki:
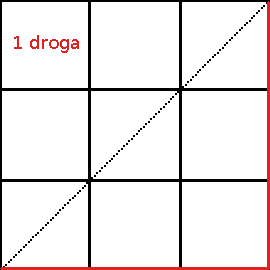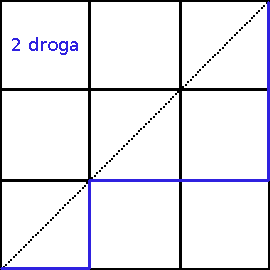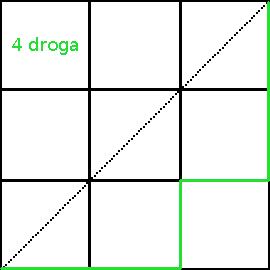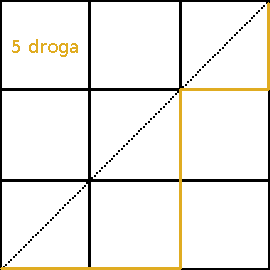
Przykład: oblicz ilość możliwych monotonicznych dróg w trójkącie równoramiennym o długości ramienia 3 i kącie prostym między ramionami. Droga ma prowadzić z jednego wierzchołka przy przeciwprostokątnej do drugiego takiego wierzchołka.
Rozwiązanie otrzymamy obliczając C3.
Nasz wynik możemy potwierdzić rozrysowując wszystkie przypadki:

Oraz inne zastosowania.