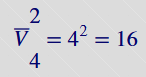W kombinatoryce mają zastosowanie różne ciekawe ciągi liczbowe. Do ich zrozumienia będzie potrzebne nam trochę podstaw:
Reguła mnożenia ▼
Polega na tym, że jeżeli pewien wybór składa się z n decyzji, przy czym pierwszy można wykonać
na k1 możliwości, drugi na k2, ... , n-ty na kn to ten wybór można
dokonać na k1*k2*...*kn sposobów.
Silnia ▼
Silnia, oznaczana symbolem ! jest to operacja matematyczna wykonywana na liczbach naturalnych, przyjmująca
wartość:
0! = 1
n! = n*(n-1)!
0! = 1
n! = n*(n-1)!
Symbol Newtona ▼
Czytany jest jako n nad k. Jest to dwu argumentowa funkcja liczb całkowitych nieujemnych, gdzie k jest mniejsze lub równe n,
zdefiniowana według wzoru:
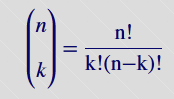
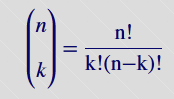
Permutacje ▼
Są to różne ustawienia kolejności elementów pewnego zbioru. Ilość permutacji bez powtórzeń elementów jest określona poniższym wzorem:
Pn=n!
Przykład: liczba możliwych kolejności ustawień liter A,B,C,D wynosi: P4=4!=24
Przykład: liczba możliwych kolejności ustawień liter A,B,C,D wynosi:
Kombinacja bez powtórzeń ▼
Jest to każdy podzbiór k-elementowy danego zbioru n-elementowego, poza zbiorem pustym
bez powtarzania elementów. Ich ilość określona jest wzorem:

Przykład: Liczba możliwych 2 znakowych wyrazów (bez możliwością powtórzenia), stworzonych z liter A,B,C,D,E wynosi:
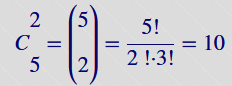

Przykład: Liczba możliwych 2 znakowych wyrazów (bez możliwością powtórzenia), stworzonych z liter A,B,C,D,E wynosi:
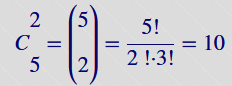
Kombinacja z powtórzeniami ▼
Jest to każdy podzbiór k-elementowy danego zbioru n-elementowego, poza zbiorem pustym
z możliwością powtarzania elementów. Ich ilość określona jest wzorem:
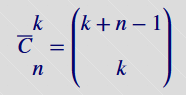
Przykład: Liczba możliwych 2 znakowych wyrazów (z możliwością powtórzenia), stworzonych z liter A,B,C,D,E wynosi:

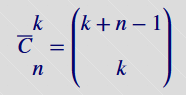
Przykład: Liczba możliwych 2 znakowych wyrazów (z możliwością powtórzenia), stworzonych z liter A,B,C,D,E wynosi:

Wariacja bez powtórzeń ▼
Jest to każdy k-elementowy ciąg różnych elementów zbioru n-elementowego. Ich ilość określona jest wzorem:
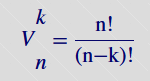
Przykład: Liczba możliwych liczb 2 cyfrowych utworzonych z cyfr 1,2,3,4 bez powtarzających się znaków wynosi: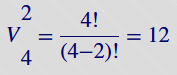
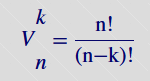
Przykład: Liczba możliwych liczb 2 cyfrowych utworzonych z cyfr 1,2,3,4 bez powtarzających się znaków wynosi:
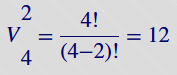
Wariacja z powtórzeniami ▼
Jest to każdy k-elementowy ciąg elementów zbioru n-elementowego(z możliwością powtórzeń). Ich ilość określona jest wzorem:
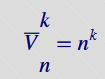
Przykład: Liczba możliwych liczb 2 cyfrowych utworzonych z cyfr 1,2,3,4(z możliwościa powtarzania się znaków) wynosi: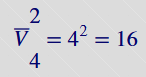
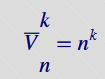
Przykład: Liczba możliwych liczb 2 cyfrowych utworzonych z cyfr 1,2,3,4(z możliwościa powtarzania się znaków) wynosi: