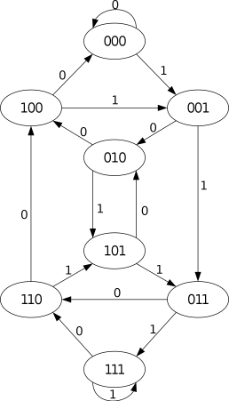
Podstawowe typy grafów.

Uproszczona definicja grafu

Graf (ang. graph) to zbiór wierzchołków (ang. node, vertex), które mogą być połączone krawędziami (ang. edge), w taki sposób, że każda krawędź kończy się i zaczyna w którymś z wierzchołków. Na rysunku obok wierzchołki reprezentowane są przez zielone koła, a krawędzie jako łączące je linie. Za pierwszego badacza grafów uważa się Leonharda Eulera, jego praca opisująca zagadnienia mostów królewieckich opublikowana w 1736 roku jest uznawana za pierwszą pracę na temat teorii grafów. Niektórzy autorzy stosują różne sposoby definiowania, opisywania i oznaczania elementów grafów.

Graf prosty (nieskierowany)

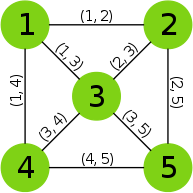
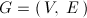
Graf nieskierowany (ang. undirected graph) to graf, w którym występują jedynie krawędzie, które można przebywać w dowolnym kierunku. Matematycznie reprezentowany jest on zwykle jako uporządkowana para dwóch zbiorów. 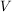- zbiór wszystkich wierzchołków grafu,
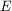- zbiór wszystkich krawędzi między różnymi wierzchołkami grafu, czyli dwuelementowych podzbiorów zbioru.
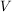Żeby lepiej zobrazować matematyczną definicję grafu, oznaczyłem krawędzie i wierzchołki poprzedniego grafu. Zatem:

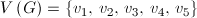
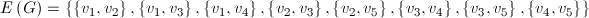
Graf skierowany (digraf)

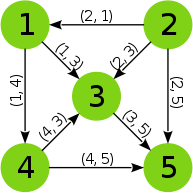
Graf 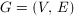, w którym krawędzie mogą być przebywane tylko w jednym kierunku nazywamy grafem skierowanym lub digrafem (ang. directed graph, digraph). Zwykle krawędzie skierowane (zwane również łukami) oznaczane są graficznie jako strzałki. Przyjmuje się, że krawędź 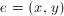jest skierowana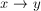. Istnieją również grafy mieszane (ang. mixed graph), posiadające krawędzie zarówno skierowane, jak i nieskierowane. Grafy mieszane opisujemy trzema zbiorami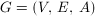, gdzie zbiór 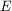jest zbiorem krawędzi nieskierowanych, a zbiór 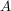wzorem krawędzi skierowanych. Jak w poprzednim przykładzie wzbogaciłem graf o strzałki, warto zwrócić uwagę na to, że również krawędzie są inaczej opisane, mimo tego, że wierzchołki pozostały bez zmian. Zbiory opisujące ten graf przedstawiają się następująco:

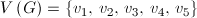
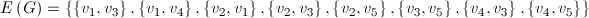
Graf ważony

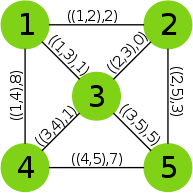
Z krawędziami grafu można dodatkowo powiązać pewne wartości, nazywane wagami. Może to być na przykład odległość pomiędzy wierzchołkami. Graf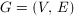, w którym takie wartości występują nazywamy grafem ważonym (ang. weighted graph). Grafem ważonym może być zarówno graf skierowany (ang. weighted digraph), nieskierowany (ang. undirected weighted graph) i mieszany (ang. weighted mixed graph). W tym konkretnym przykładzie posłużę się grafem nieskierowanym. Graf ten można opisać następująco:

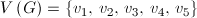
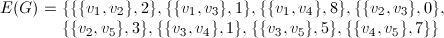
Podstawowe pojęcia służące do opisu grafów.

Ścieżka (ang. path)

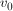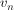W teorii grafów ścieżką łączącą z o długości nazywamy ciąg wierzchołków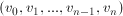 taki, że dla każdego 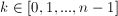istnieje krawędź z 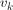do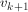. Często jako ścieżkę rozumiemy ciąg lub zbiór krawędzi łączących kolejne wierzchołki w ciągu wierzchołków ścieżki. Ścieżkę, w której nie ma powtarzających się wierzchołków, z wyjątkiem ewentualnej równości pierwszego i ostatniego wierzchołka, nazywamy drogą. Droga, w której 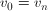jest zwana drogą zamkniętą, czyli tzw. cyklem (ang. cycle). W przypadku krawędzi grafów ważonych należy odróżnić pojęcie długości od odległości. Odległością nazywamy sumę wag krawędzi łączących kolejne wierzchołki na ścieżce.

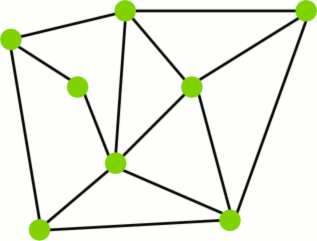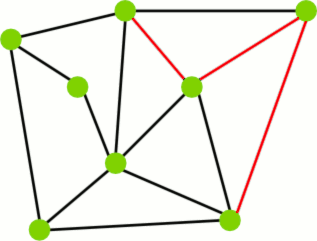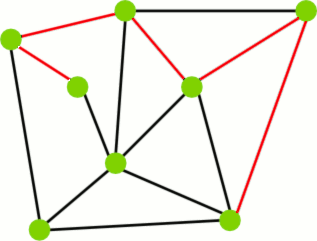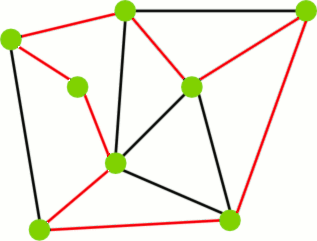
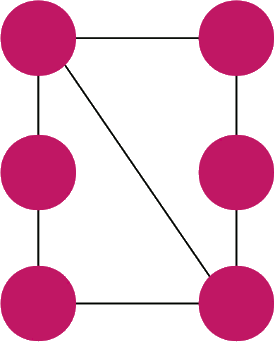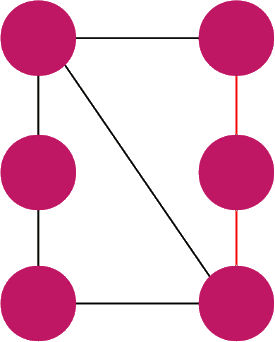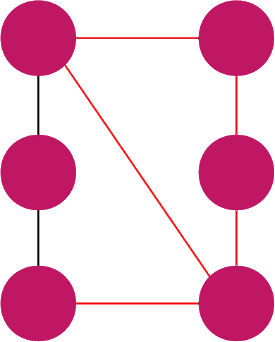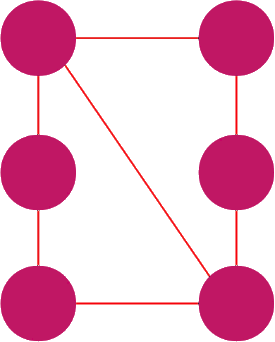
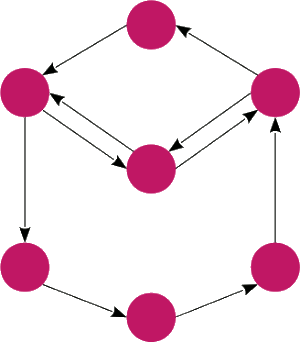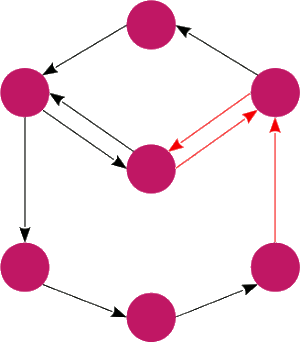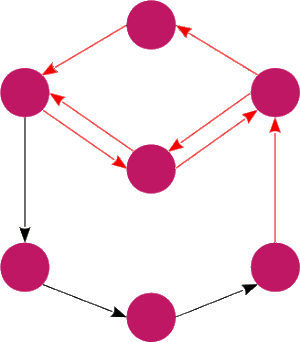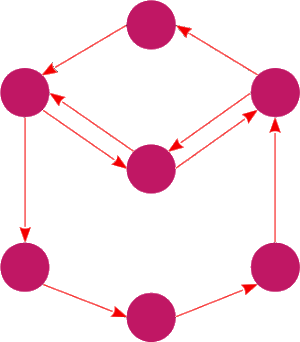
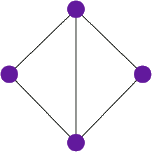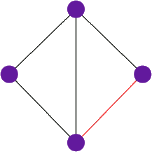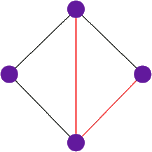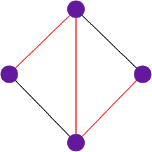
Przykład cyklu.

Stopień wierzchołka

Stopniem wierzchołka nazywamy liczbę kończących się w nim krawędzi i oznaczamy, jako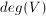. W przypadku grafów skierowanych wyróżniamy stopień wejściowy - 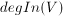oraz wyjściowy -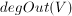. Wierzchołki o stopniu 0, czyli nie będący końcem żadnej krawędzi nazywamy wierzchołkiem izolowanym.

Pętla

Krawędź, która zaczyna i kończy się w tym samym wierzchołku.

Sąsiad

Dwa wierzchołki nazywamy sąsiadami, jeśli pomiędzy nimi istnieje krawędź.

Graf podstawowy

Graf podstawowy grafu skierowanego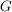 to graf nieskierowany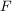, w którym pomiędzy dwoma wierzchołkami a, b istnieje krawędź wtedy i tylko wtedy, gdy w grafie 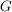istnieje krawędź od a do b lub od b do a. Tworzenie grafu podstawowego można rozumieć jako usuwanie grotów z krawędzi grafu skierowanego.

Spójność grafu

Graf nazywamy spójnym, jeżeli dla dowolnej pary wierzchołków istnieje ścieżka, która je łączy.

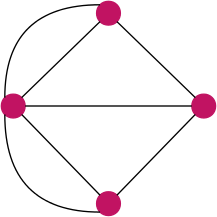
Graf pełny

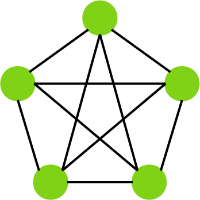
Grafem pełnym nazywamy graf prosty, w którym dla każdej pary wierzchołków istnieje krawędź je łącząca. Graf pełny o wierzchołkach oznaczamy Kn. Własności grafów pełnych:

  • pełny graf o wierzchołkach posiada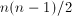 krawędzi,
  • wszystkie grafy pełne są swoimi klikami,
  • żaden z grafów pełnych stopnia co najmniej 5 nie jest grafem planarnym,

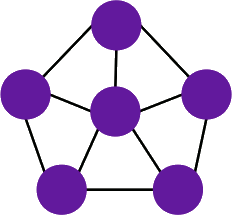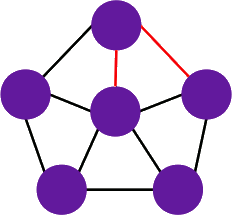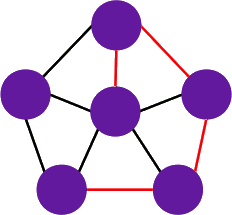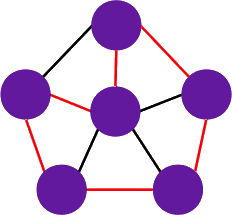
Graf regularny

Grafem regularnym stopnia nazywamy graf, w którym wszystkie wierzchołki są stopnia, czyli z każdego wierzchołka grafu regularnego wychodzi krawędzi. Graf regularny stopnia określa się często grafem-regularnym.

Klika

Mianem kliki w teorii grafów określamy podgraf, w którym każde dwa wierzchołki połączone są krawędzią.

Graf planarny

Grafem planarnym nazywamy graf, który można narysować na płaszczyźnie tak, by krzywe obrazujące jego krawędzie nie przecinały się ze sobą. Jego odwzorowanie na płaszczyźnie nazywamy rysunkiem płaskim.

Grafy eulerowski, cykl Eulera

Problem mostów w Królewcu

W Królewcu, na rzece Pergole, na której są dwie wyspy (reprezentowane przez lewy i prawy wierzchołek grafu obok), wybudowano siedem mostów łączących je z brzegami (reprezentowane przez górny oraz dolny wierzchołek grafu obok) oraz ze sobą. Mieszkańcy Królewca postawili Eulerowi pytanie, czy można tak ułożyć spacer, aby przejść po wszystkich mostach dokładnie raz i wrócić do punktu startu. Matematyk oczywiście odpowiedział na to pytanie przecząco, ponieważ nie jest to możliwe. W 1736 roku Euler wydał swoje dzieło, opisujące rozwiązanie tego problemu.

Ścieżka i cykl Eulera w grafie nieskierowanym

Ścieżką Eulera w grafie nieskierowanym nazywamy ścieżkę, przechodzącą po każdej krawędzi grafu, dokładnie jeden raz. Można ją skonstruować jedynie, jeżeli co najwyżej dwa wierzchołki mają nieparzysty stopień. Cykl Eulera jest ścieżką Eulera zaczynającą się i kończącą w tym samym wierzchołku grafu. Aby można było skonstruować ścieżkę Eulera wszystkie wierzchołki grafu muszą mieć parzysty stopień. Graf, w którym występuje ścieżka, lecz nie występuje cykl Eulera nazywamy grafem półeulerowskim, natomiast graf posiadający cykl Eulera nazywamy grafem Eulerowskim.

Przykład grafu eulerowskiego z zaznaczonym cyklem Eulera.

Przykład grafu półeulerowskiego z zaznaczoną ścieżką Eulera.

Ścieżka i cykl Eulera w grafie skierowanym

W grafie skierowanym ścieżką Eulera nazywamy ścieżkę, przechodzącą po każdej krawędzi grafu dokładnie jeden raz. Analogicznie do poprzedniej definicji cykl Eulera w grafie skierowanym definiujemy jako ścieżkę Eulera zaczynającą się i kończącą w tym samym wierzchołku. Graf posiada ścieżkę Eulera, jeśli wszystkie wierzchołki, z wyjątkiem dwóch mają takie same stopnie wejścia i wyjścia, w jednym z dwóch pozostałych wierzchołków stopień wejścia jest o 1 wyższy niż wyjścia, w drugim odwrotnie. Cykl Eulera istnieje, jeśli stopnie wejściowy i wyjściowy wszystkich wierzchołków są sobie równe, czyli liczba krawędzi wchodzących jest równa liczbie krawędzi wychodzących z wierzchołka.

Przykład skierowanego grafu eulerowskiego z zaznaczonym cyklem Eulera.

Grafy hamiltonowskie, cykl Hamiltona

Problem komiwojażera

Aby lepiej zrozumieć definicję cyklu Hamiltona warto zapoznać się z problemem komiwojażera, który chce odwiedzić wszystkich swoich klientów tylko jeden raz. Klientów będziemy reprezentować jako wierzchołki grafu, a drogi między nimi jako krawędzie. Problem polega na wyznaczeniu drogi tak, aby w każdym wierzchołku znaleźć się tylko jeden raz. Często w problemie komiwojażera występuje graf ważony, który dodatkowo utrudnia rozwiązanie problemu, ponieważ musimy znaleźć ścieżkę Hamiltona o możliwie najmniejszej sumie wag przebywanych krawędzi. Po prawej stronie na obrazku znajduje się przykładowa ścieżka Hamiltona.

Cykl Hamiltona w grafie nieskierowanym

Ścieżka Hamiltona to ścieżka przechodząca przez każdy wierzchołek Grafu dokładnie jeden raz. Ścieżkę Hamiltona zaczynającą się i kończącą w tym samym wierzchołku nazywamy cyklem Hamiltona, a graf, który posiada taki cykl - grafem hamiltonowskim. Podobnie jak w poprzednim przypadku graf posiadający jedynie ścieżkę Hamiltona nazywamy grafem półhamiltonowskim.

Przykład grafu hamiltonowskiego z zaznaczonym cyklem Hamiltona.

Warunki wystarczające

Gdy rozważaliśmy grafy Eulera mieliśmy jasno określony warunek, kiedy graf jest grafem eulerowskim lub półeulerowskim. W przypadku grafów Hamiltona niestety nie jest znana żadna metoda pozwalająca szybko stwierdzić, czy dany graf jest hamiltonowski. Istnieją jednak warunki pozwalające stwierdzić jednoznacznie, że dany graf jest hamiltonowski. Należy jednak pamiętać, że jest to jedynie jednostronna implikacja, tzn. istnieje nieskończenie wiele grafów, nie posiadającej żadnej z poniższych cech. Przykładowo powyższy graf nie spełnia ostatniego twierdzenia.

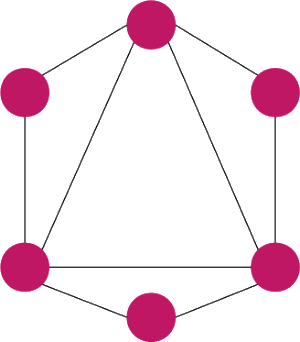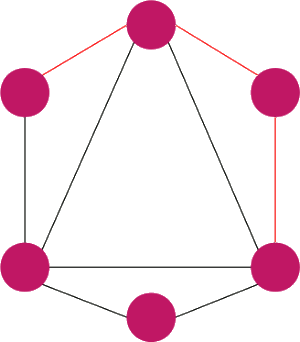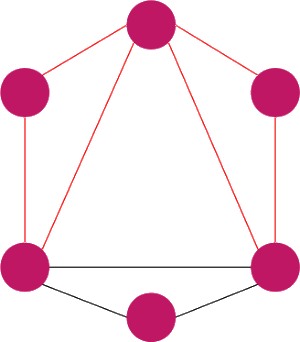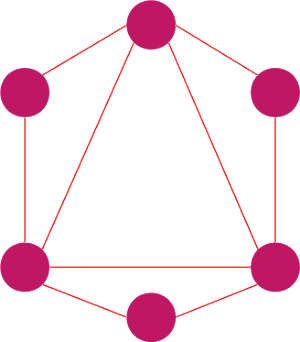
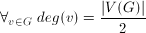Twierdzenie Diraca - Jeśli graf G nie ma pętli, ani krawędzi wielokrotnych, posiada więcej niż trzy wierzchołki oraz to graf jest hamiltonowski.

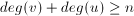Twierdzenie Ore - Jeżeli w grafie prostym G o wierzchołkach, n>2 zachodzi następująca równość dla każdej pary niepołączonych bezpośrednio krawędzią wierzchołków u i v, to graf G posiada cykl Hamiltona.

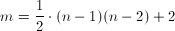Twierdzenie o liczbie krawędzi - Jeśli graf prosty o wierzchołkach ma co najmniej m krawędzi, gdzie:, to jest hamiltonowski

Grafy de Bruijna, cykl de Bruijna

Cykl de Bruijna

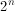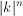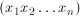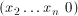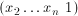Cyklem (lub ciągiem) de Bruijna rzędu nazywamy cykliczny zero-jedynkowy ciąg długości , w którym każdy podciąg kolejnych elementów występuje co najwyżej raz. Przykłady cykli de Bruijna dla małych wartości n:

Ciąg de Bruijna możemy rozszerzyć na bardziej liczne alfabety niż tylko zero-jedynkowy. Wtedy wprowadzamy zbiór k, będący naszym alfabetem. Ciąg de Bruijna w takim wypadku ma długość.

Wyznaczanie ciągu de Bruijna za pomocą grafu de Bruijna

Chcąc wygenerować ciąg de Bruijna możemy posłużyć się grafem de Bruijna. Jego wierzchołki etykietujemy wszystkimi możliwymi słowami binarnymi długości n. Krawędzie natomiast etykietujemy symbolami z alfabetu. Aby skonstruować taki graf postępujemy według reguły:

Graf de Bruijna dla n=3.

Zastosowania ciągów de Bruijna