Figury Niemierzalne
Wstęp
Czytając tytuł tej strony można wpaść w lekką konsternację. O co tu chodzi? Co można zmierzyć w figurze? Długości odcinków? Miary kątów wewnętrznych? Pole?
Zajmijmy się może na chwilę długością odcinków:
 Intuicyjnie każdy może stwierdzić, że odległość od punktu A do punktu A wynosi 0, natomiast długość odcinka AB wynosi 1.
Intuicyjnie każdy może stwierdzić, że odległość od punktu A do punktu A wynosi 0, natomiast długość odcinka AB wynosi 1.
Zaznaczmy na osi liczbowej zbiór punktów, których współrzędne są liczbami wymiernymi.
 Jaka jest długość tego zbioru? Każdy z pewną znajomością matematyki wie, że
między dowolnymi dwiema liczbami wymiernymi jest nieskończenie wiele liczb wymiernych. Oznacza to, że na między każdymi dwoma punktami należałoby wstawić
nieskończenie wiele punktów, czego nie da się przedstawić na żadnej animacji. Czy jednak zostały zaznaczone wszystkie punkty odcinka AB? Oczywiście nie, gdyż
istnieją również punkty o współrzędnych niewymiernych. To dość ciekawe, że 'nieskończenie wiele' nie oznacza 'wszystkie'. Żeby było jeszcze ciekawiej, to w oparciu
o teorię zbiorów można wykazać, że punktów o współrzędnych niewymiernych jest więcej od punktów o współrzędnych wymiernych.
Jaka jest długość tego zbioru? Każdy z pewną znajomością matematyki wie, że
między dowolnymi dwiema liczbami wymiernymi jest nieskończenie wiele liczb wymiernych. Oznacza to, że na między każdymi dwoma punktami należałoby wstawić
nieskończenie wiele punktów, czego nie da się przedstawić na żadnej animacji. Czy jednak zostały zaznaczone wszystkie punkty odcinka AB? Oczywiście nie, gdyż
istnieją również punkty o współrzędnych niewymiernych. To dość ciekawe, że 'nieskończenie wiele' nie oznacza 'wszystkie'. Żeby było jeszcze ciekawiej, to w oparciu
o teorię zbiorów można wykazać, że punktów o współrzędnych niewymiernych jest więcej od punktów o współrzędnych wymiernych.
Podsumowując: między każdymi dwoma punktami o współrzędnych wymiernych istnieje nieskończenie wiele punktów o współrzędnych wymiernych oraz "jeszcze więcej" punktów o współrzędnych niewymiernych.
Jaka jest zatem długość tego zbioru? 1 to chyba trochę za dużo, a 0 to trochę za mało. Jakakolwiek propozycja nie daje się uzasadnić. Można więc podejrzewać, że tego zbioru nie da się zmierzyć!
Jedynym sposobem aby to wykazać jest wykorzystanie definicji miary (długości), jednakże nie jest ona łatwa, dlatego w tej pracy posłużę się miarą bardziej obrazową, a mianowicie polem powierzchni.
Pole Powierzchni
Od najmłodszych lat wyznaczaliśmy przybliżone pola powierzchni różnych figur, jednak na pytanie czym jest pole powierzchni większość z nas milknie lub próbuje zdefiniować pole konkretnej figury.
Jako, że matematyka na funkcji stoi, to pole powierzchni jest oczywiście funkcją, która pewnej rodzinie figur przyporządkowuje liczby rzeczywiste.
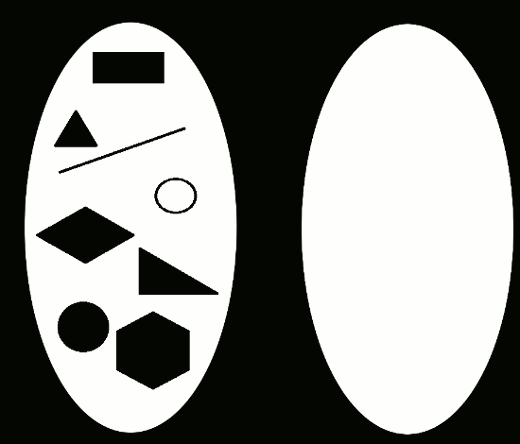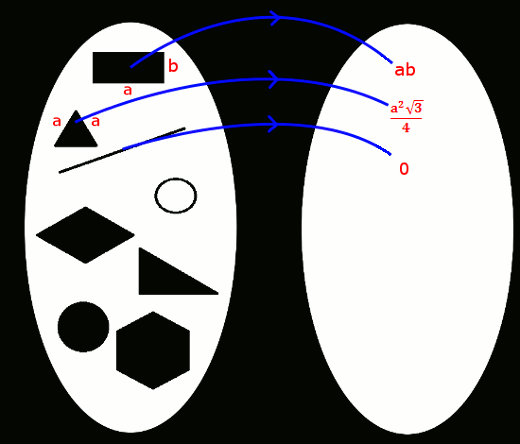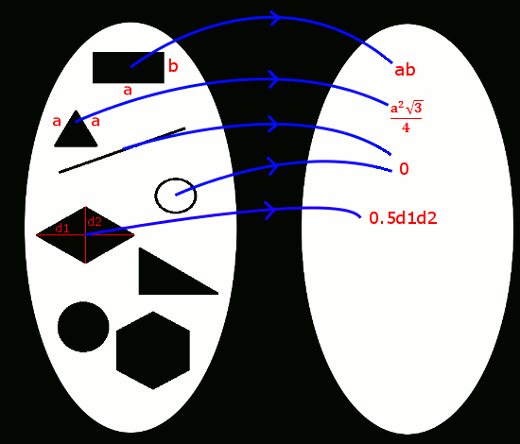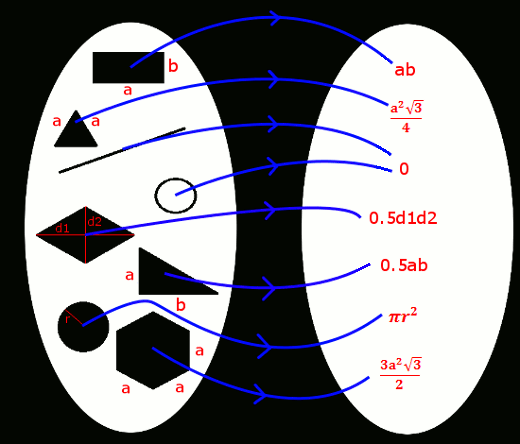
Czy jednak jest to dowolna funkcja? Oczywiście nie - musi ona spełniać pewne warunki:
1. Pola figur należą do zboiru liczb nieujemnych
2. Pole kwadratu o boku 1 wynosi 1
3. Pole sumy figur rozłącznych jest równe sumie pól tych figur
W zapisie symbolicznym:

Pole to funkcja, której dziedziną jest pewna rodzina figur. Jaka rodzina? To pytanie zbliża już nas do tematyki tej prezentacji, jednak aby na nie odpowiedzieć, musimy odpowiedzieć na inne pytanie, mianowicie jak mierzymy pole?
Jak zmierzyć pole powierzchni?
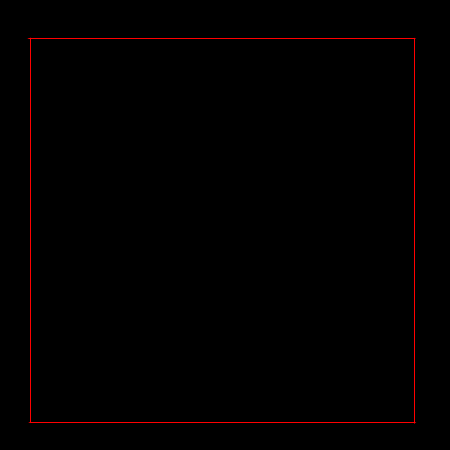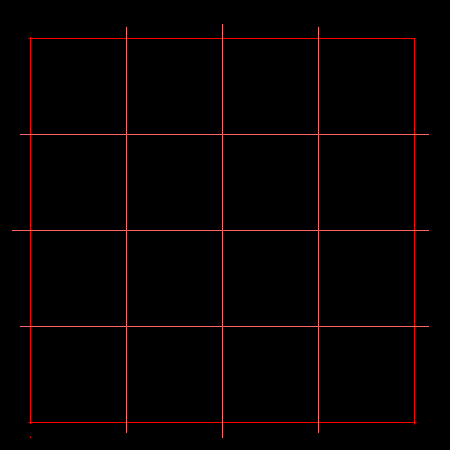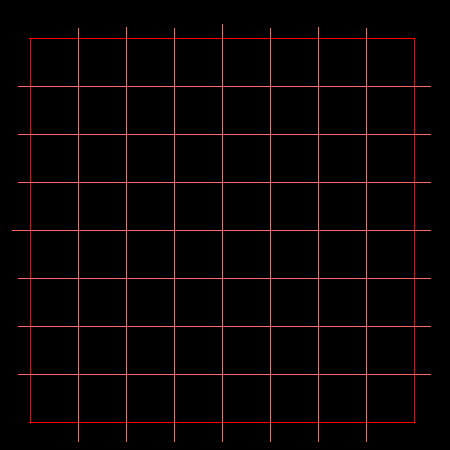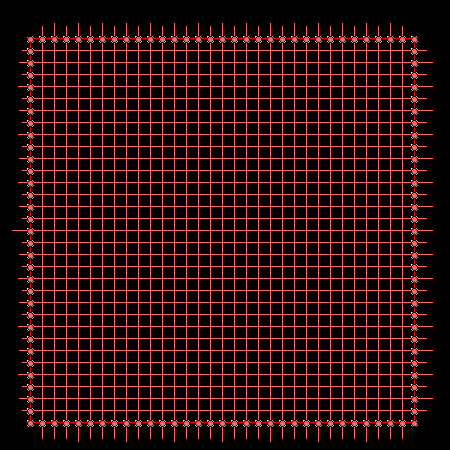
Przypomnijmy sobie jak wyznaczaliśmy (przybliżone) pole powierzchni figur na samym początku naszej edukacji matematcznej.
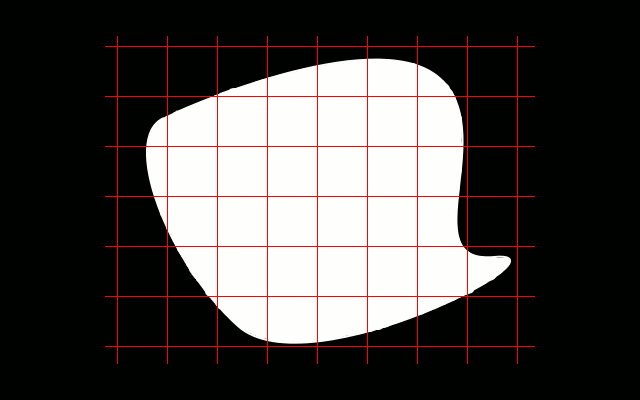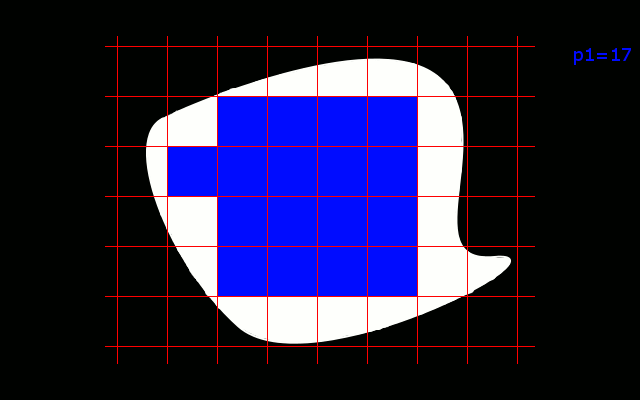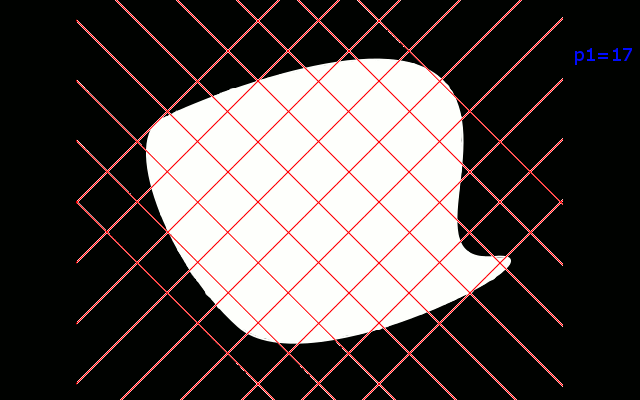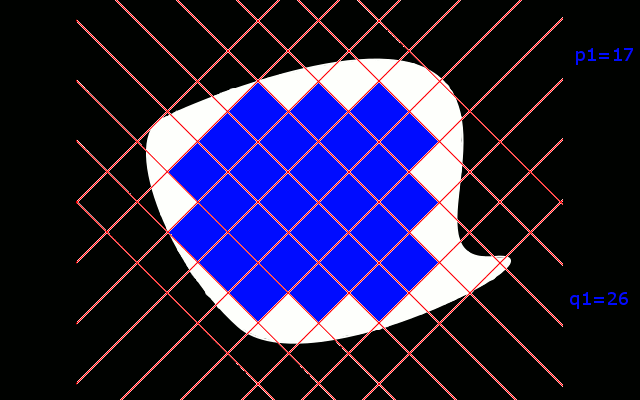
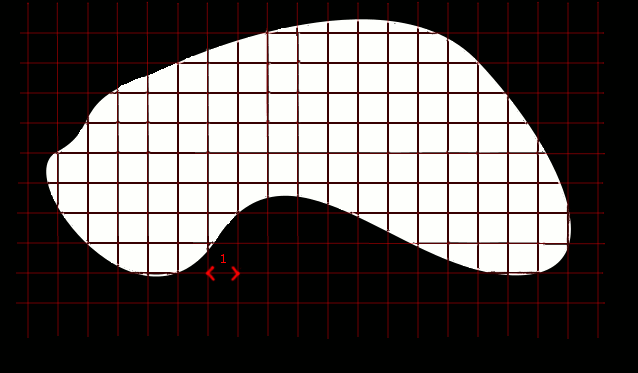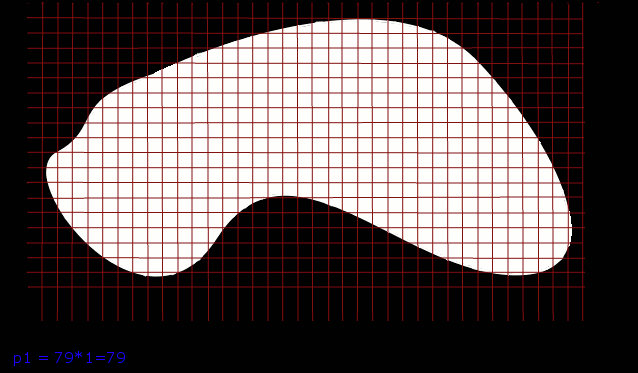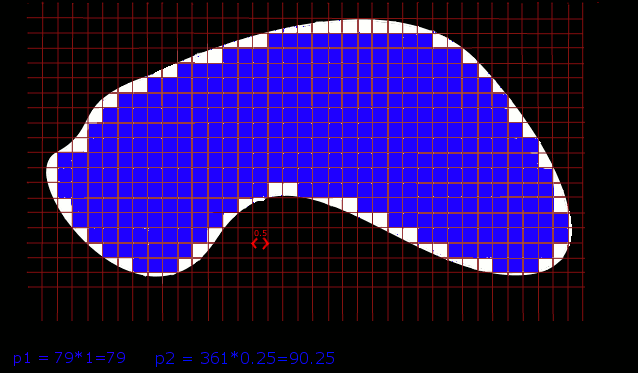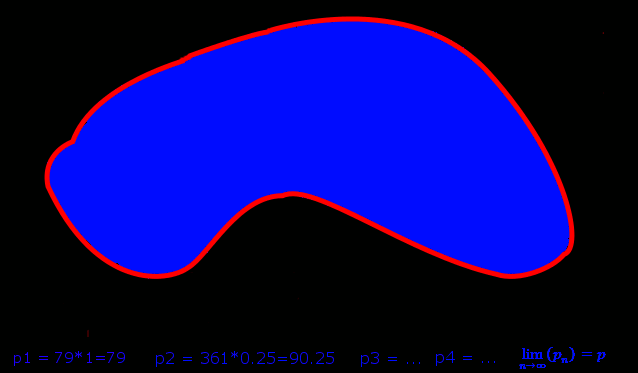 Badaliśmy na przykład ile kwadratów o boku 1 'mieści' się w tej figurze.Ich ilosć była naszym polem polem powierzchni, które oznaczmy p1.
Badaliśmy na przykład ile kwadratów o boku 1 'mieści' się w tej figurze.Ich ilosć była naszym polem polem powierzchni, które oznaczmy p1.
Na rysunku widać jednak część figury, która nie znajduje się we wnętrzu żadnego z kwadratów.
Narzućmy zatem siatkę o dwa razy większym zagęszczeniu kwadratów. Tym razem ich ilość będzie większa, a bok i pole mniejsze. Sumę ich pól oznaczmy p2.
Niestety, wciąż pewna część figury nie należy do wnętrza
żadnego z kwadratów. Po kolejnych podwojeniach zagęszczenia siatki otrzymujemy pewne przybliżenia pola p3, p4, p5, ...
Niektórzy pewnie zauważyli, że otrzymaliśmy nieskończony ciąg przybliżeń:
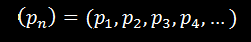
Jego wyrazy dążą do pola tej figury, które oznaczmy p, zatem:
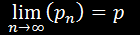
Teoretycznie zmierzyliśmy pole powierzchni tej figury, ale czy na pewno?
Przede wszystkim jeśli zamiast podwajać zagęszczenie kwadratów, będziemy je potrajać, to otrzymamy zupełnie inny ciąg. Zmieniać zagęszczenie siatki możemy w dowolny sposób, więc takich ciągów jest nieskończenie wiele.
Ponadto, jeśli zmienimy położenie siatki (lub nałożymy ją pod innym kątem), to każde przybliżenie naszego pola może być
inne od odpowiadającego im przybliżenia, gdy siatka była w położeniu pierwotnym.
Otrzymamy zatem zupełnie inny ciąg:

Można jednak zauważyć, że jego wyrazy również dążą do p:
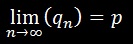
Położenie siatek może być dowolne, zatem istnieje nieskończenie wiele ciągów przybliżeń pola powierzchni.
Jeśli granicą każdego z nich jest ta sama liczba p,
to mamy zmierzone pole powierzchni, prawda?
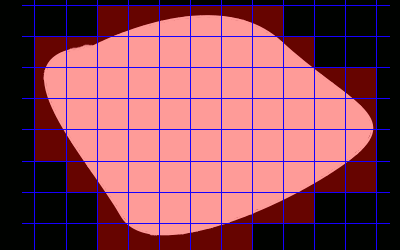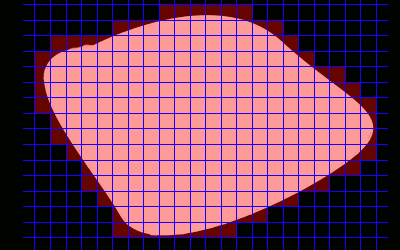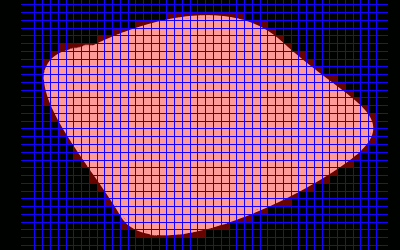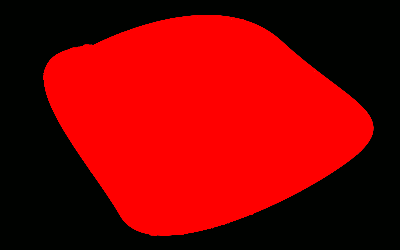 No cóż, jak dotąd przybliżaliśmy pole powierzchni od wewnątrz, ale możemy to również zrobić od zewnątrz, licząc ilosć kwadracików,
No cóż, jak dotąd przybliżaliśmy pole powierzchni od wewnątrz, ale możemy to również zrobić od zewnątrz, licząc ilosć kwadracików,
w których zawiera się nasza figura.
Otrzymujemy kolejny ciąg (a właściwie nieskończenie wiele ciągów,
bo położenie siatki ponownie jest dowolne),
którego wyrazy dążą do liczby p.
Dopiero teraz, gdy wszystkie ciągi 'od wewnątrz' figury oraz 'od zewnątrz' są zbieżne do tej samej liczby p, to pole powierzchni figury jest równe właśnie p.
Innymi słowy jeśli miara wewnętrzna tej figury jest równa mierze zewnętrznej, to ta figura posiada pole powierzchni, czyli jest zmierzalna (wg miary Jordana).
Wracając do definicji pola: Pole to funkcja, której dziedziną jest pewna rodzina figur, a przeciwdziedziną - zbiór liczb rzeczywistych.
Tą rodziną są właśnie
figury mierzalne (wg miary Jordana). A co z resztą? Czy istnieją figury, które nie są mierzalne, więc nie mają pola powierzchni? Otóż istnieją i teraz, po tym
przydługawym, acz potrzebnym wprowadzeniu zamierzam kilka z nich zdefiniować.
Figura niemierzalna - kwadrat sito
W matematyce, definicja figury to podanie sposobu jej konstrukcji. Oto konstrukcja figury zwanej kwadratem sito:
 Niestety kolejne kroki już są z oczywistych względów niemożliwe do pokazania na ekranie kompuera. Nie znaczy to jednak, że nie możemy powtarzać tych czynności 10, 1000, dowolną ilosć razy.
Natomiast figurę, którą otrzymamy wykonując podane czynności nieskończenie wiele razy nazywamy kwadratem sito.
Niestety kolejne kroki już są z oczywistych względów niemożliwe do pokazania na ekranie kompuera. Nie znaczy to jednak, że nie możemy powtarzać tych czynności 10, 1000, dowolną ilosć razy.
Natomiast figurę, którą otrzymamy wykonując podane czynności nieskończenie wiele razy nazywamy kwadratem sito.
Figury tej nie można narysować ani nawet sobie jej wyobraźić, jednak z matematycznego punktu widzenia ona istnieje, gdyż podaliśmy sposób jej konstrukcji.
Należałoby teraz udowodnić, że jest to niemierzalna, a więc nie ma pola powierzchni. Dowód ten będzie się opierał na powyższych informacjach.
 Weźmy kwadracik o dowolnie małym boku 1/m, gdzie m jest dość dużą liczbą.
Weźmy kwadracik o dowolnie małym boku 1/m, gdzie m jest dość dużą liczbą.
Ile takich malutkich kwadracików o takim boku zawiera się w naszym kwadracie sito? Może żaden?
Jeśli tak, to w każdym takim kwadraciku zawiera sie punkt, który został usunięty z kwadratu sito.
Spróbujmy to wykazać:
Oto fragment kwadratu sito w k-tym kroku, w bardzo dużym przybliżeniu. Wstawmy nasz kwadracik w dowolne miejsce.
Póki co, żaden 'wyrzucony' punkt się w nim nie zawiera,
lecz to jest dopiero k-ty krok konstrukcji kwadratu sito, a ich jest nieskończenie wiele. Jeśli więc wykonamy kolejne kroki konstrukcji, to zauważymy, że już
w k+2 kroku w naszym małym kwadraciku pojawił się punkt, który został wyrzucony z kwadratu sito.
Zatem nasz kwadracik nie zawiera się w kwadracie sito, a zważywszy na to, że rozpatrywaliśmy kwadraciki o dowolnie małym boku, to możemy wywnioskować, że nie ma żadnego kwadracika, który byłby zawarty w tej figurze.
Skoro tak, to miara wewnętrzna kwadratu sito wynosi 0. Natomiast dość oczywisty jest fakt, że jego miara zewnętrzna wynosi 1.
Zatem miara zewnętrzna nie jest równa mierze wewnętrznej, a więc kwadrat sito nie posiada pola powierzchni i jest niemierzalny według miary Jordana.
Własności kwadratu sito
Kwadrat sito jako figura dość niezwykłą posiada dość niezwykłe właściwości:
 Policzmy ile punktów zostało wyrzucone z kwadratu sito w 5 kroku:
Policzmy ile punktów zostało wyrzucone z kwadratu sito w 5 kroku:
1+4+16+64+256=341
Warto zauważyć, że kolejne liczby są kwadratami kolejnych potęg dwójki:
(20)2+(21)2+(22)2+(23)2+(24)2=341
W szóstym kroku wyrzucilibyśmy (25)2 punktów, w siódmym - (26)2, a w n-tym - (2n-1)2
Zatem po n-krokach z kwadratu zostanie wyrzucone:
Sn = (20)2+(21)2+(22)2+(23)2+(24)2+...+(2n-1)2
Jeśli zapiszemy to inaczej: Sn = 20+22+24+26+...+22n-2, to można zauważyć, że jest to ciąg geometryczny o pierwszym wyrazie równym 1 oraz ilorazie równym 22.
Korzystając ze znanego wzoru na sumę ciągu otrzymujemy:
1*((22)n-1)/(22-1) = 1/3(4n-1)
Zatem ilość wyrzucanych punktów rośnie wręcz lawinowo, gdyż już w 150-tym kroku otrzymamy niewyobrażalną liczbę 1/3(2^300-1), która jest większa od szacowanej przez naukowców liczby atomów we wszechświecie.
A to był dopiero 150-ty krok, a mamy ich wykonać nieskończenie wiele.
Wykazaliśmy wyżej, że nie istnieje żaden kwadrat o dowolnie małym boku, który by się zawierał w kwadracie sito. Czy jednak istnieje odcinek, który w całości zawierałby się w naszej figurze? Oczywiście, że tak - spójrzmy na nią jeszcze raz:
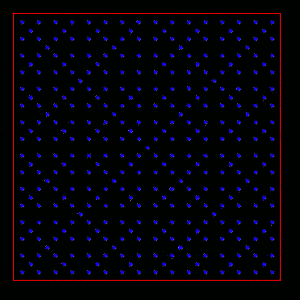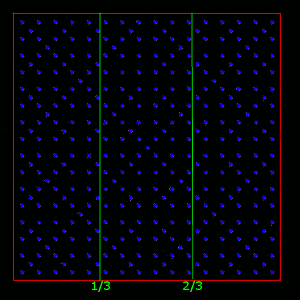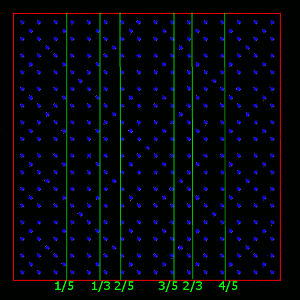 Jeśli bok kwadratu sito przedstawimy jako przedział <0;1>, to można zauważyć, że pionowe odcinki, z których usuwamy punkty to:
Jeśli bok kwadratu sito przedstawimy jako przedział <0;1>, to można zauważyć, że pionowe odcinki, z których usuwamy punkty to:
1/2, 1/4, 3/4, 1/8, 3/8, 5/8, 7/8
Ogólnie: k/2n, gdzie k i n należą do Naturalnych i k < 2n
Czy zatem istnieją jakieś odcinki z których nie zostanie usunięty żaden punkt?
Otóż istnieją i jest ich nieskończeniele wiele. Będą to wszystkie ułamki, których nie da się przedstawić w postaci k/2n, na przykład:
1/3, 2/3, 1/5, 2/5, 3/5, 4/5...
Co więcej, między każdymi dwoma odcinkami, które w całości zawierają się w kwadracie sito istnieje nieskończenie wiele odcinków, które również się w nim zawierają.
Zastanówmy się jeszcze jak gęsto są rozmieszczone punkty wyrzucone z kwadratu sito.
Wiemy, że pionowe odcinki, z których usuwamy punkty dają się przedstawić w postaci k/2n. Wiemy też, że między dwoma odcinkami, z których usuwamy punkty, oddalonymi od siebie o dowolnie małą odległość istnieje nieskończenie wiele takich odcinków.
Można zatem wywnioskować, że odległości między usuwanymi punktami mogą być dowolnie małe, a więc każdy wyrzucony punkt leży w dowolnie małej odległości od innego wyrzuconego punktu.

Aby zrozumieć konsekwencje tego stwierdzenia należy przypomnieć czym są punkty brzegowe oraz brzeg figury:
Punkt jest punktem brzegowym figury jeśli w każdym otoczeniu (kole o środku w tym punkcie) tego punktu zawiera się przynajmniej jeden punkt, który do tej figury należy oraz przynajmniej jeden punkt, który do niej nie należy.
Brzegiem figury nazywamy natomiast zbiór wszystkich jej punktów brzegowych.
Wracając do kwadratu sito, skoro każdy wyrzucony punkt leży w dowolnie małej odległości od innego wyrzuconego punktu, to w każdym jego otoczeniu istnieje punkt, który do figury nie należy.
Co więcej, wiemy już, że między dwoma odcinkami, z których nie usuniemy żadnych punktów istnieje nieskończenie wiele takich odcinków.
Zatem odległość między takimi odcinkami może być dowolnie mała
, a więc w każdym otoczeniu każdego wyrzuconego punktu znajduje się również punkt, który do figury należy, zatem każdy wyrzucony punkt jest punktem brzegowym kwadratu sito.
Postępując analogicznie okazuje się, że każdy punkt, który nie został wyrzucony z figury również jest jej punktem brzegowym.
Zatem brzegiem kwadratu sito okazuje się cały kwadrat. To dość zaskakujące, że figura zawiera się w jej brzegu, a nie odwrotnie.
Inne figury niemierzalne
Oczywiście kwadrat sito nie jest jedyną figurą niemierzalną. Jest ich nieskończenie wiele.
Przede wszystkim można zmienić sposób wyrzucania punktów (na przykład zamiast dzielić boki kwadratu na połowy, to można je podzielić na 3 części):
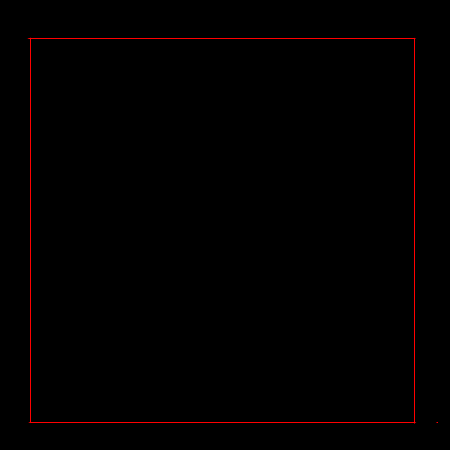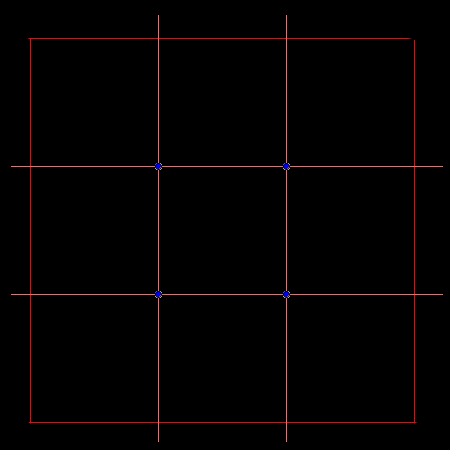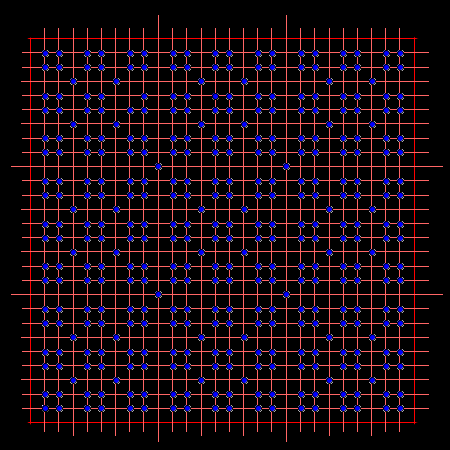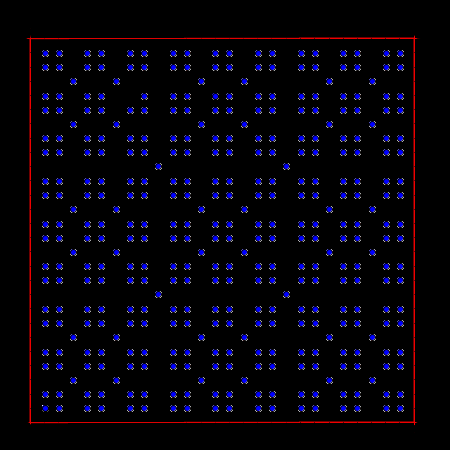
Zamiast usuwać pojedyncze punkty z kwadratu można usuwać całe odcinki, konstruując kwadrat poszatkowany:
Oczywiście każda z tych figur nie posiada pola, gdyż ich miara wewnętrzna jest różna od ich miary zewnętrznej. Przykładowo w figurze zwanej 'kwadrat z brodą':

miara wewnętrzna jest równa 1, natomiast miara zewnętrzna - 2.
Oczywiście wszystkie figury na powyższych animacjach są skonstruowane tylko do pewnego kroku. Aby otrzymać figurę niemierzalną należałoby postępować analogicznie nieskończenie wiele razy.
Figury niemierzalne są dość niezwykłe i posiadają dość nieprawdopodobne własności. Nie jesteśmy ich w stanie narysować ani nawet sobie ich wyobraźić.
Jest to świetny przykłąd na to, że matematyka potrafi zaskoczyć na każdym kroku
Opracował: Bochenek Piotr




 Badaliśmy na przykład ile kwadratów o boku 1 'mieści' się w tej figurze.Ich ilosć była naszym polem polem powierzchni, które oznaczmy p1.
Badaliśmy na przykład ile kwadratów o boku 1 'mieści' się w tej figurze.Ich ilosć była naszym polem polem powierzchni, które oznaczmy p1.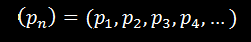
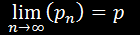


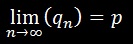
 No cóż, jak dotąd przybliżaliśmy pole powierzchni od wewnątrz, ale możemy to również zrobić od zewnątrz, licząc ilosć kwadracików,
No cóż, jak dotąd przybliżaliśmy pole powierzchni od wewnątrz, ale możemy to również zrobić od zewnątrz, licząc ilosć kwadracików,
 Weźmy kwadracik o dowolnie małym boku 1/m, gdzie m jest dość dużą liczbą.
Weźmy kwadracik o dowolnie małym boku 1/m, gdzie m jest dość dużą liczbą. Policzmy ile punktów zostało wyrzucone z kwadratu sito w 5 kroku:
Policzmy ile punktów zostało wyrzucone z kwadratu sito w 5 kroku: Jeśli bok kwadratu sito przedstawimy jako przedział <0;1>, to można zauważyć, że pionowe odcinki, z których usuwamy punkty to:
Jeśli bok kwadratu sito przedstawimy jako przedział <0;1>, to można zauważyć, że pionowe odcinki, z których usuwamy punkty to:


