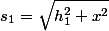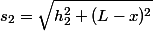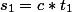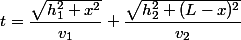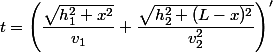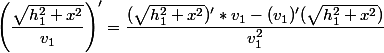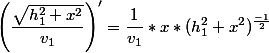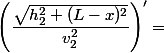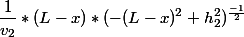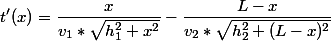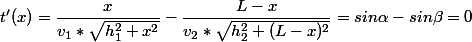Zadanie: Wykaż, że światło odbijające się od płaskiego zwierciadła biegnie po takiej drodze, że czas potrzebny na jej przebycie jest najkrótszy.

Zaczniemy od narysowania rysunku pomocniczego do zadania:



1) Rysujemy ramy tak jak na animacji
2) Zaznaczamy punkty A i B i odcinki oznaczające drogę światła. Korzystamy z zasady: "Kąt odbicia jest równy kątowi padania".
3) Zaznaczamy odpowiednie kąty tak jak na animacji.
4) Podobnie zaznaczamy potrzebne wielkości fizyczne.
h₁, h₂ - wysokości punktów A i B
s₁, s₂ - droga światła od A do zwierciadła i od zwierciadła do B









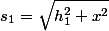
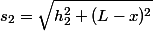
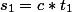
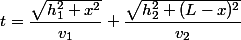
gdzie v₁ i v₂ są prędkością światła

Posiadając takie dane z łatwością możemy wyprowadzić pochodną t'(x).



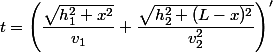
Policzmy oddzielnie pochodne:





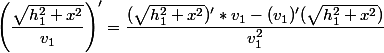
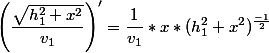
Zauważ że x²+h² pod pierwiastkiem to funkcja złożona (funkcja z funkcji) Dlatego należy zastosowac wzór pochodnej funkcji złożonej.

Analogicznie obliczamy drugą część pochodnej:

  

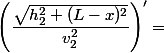
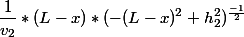
Jako, że v₁ i v₂ to prędkości światła, możemy zapisać je jako c.

Cała pochodna t'(x) wynosi:



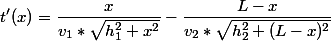
Przyjżyj się rysunkowi. Czym jest ta pochodna? Okazuje się, że:



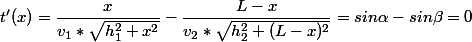
Korzystając z twierdzenia, że kąt odbicia jest równy kątowi padania wnioskujemy, że kąty α i β mają równe miary (co za tym idzie takie same sinusy) co oznacza, że pochodna ta zawsze będzie równa 0.

Gdy pochodna funkcji jest równa 0 możemy sprawdzić czy to ekstremum korzystając z drugiej pochodnej.(pochodnej z pierwszej pochodnej) Gdy jest ona większa od 0 jest to minimum a gdy mniejsza to maksimum. Gdy jest równa 0 jest to punkt przegięcia.



Jako, że wysokości h₁, h₂ i odległości x i L-x są większe od 0 (inaczej odbicie światła nie miałoby sensu) to druga pochodna jest dodatnia.

Wniosek?

Czas jest zawsze najkrótszy z możliwych.