Zadanie: Jaki promień powinna mieć puszka o objętości 54π aby przy jej produkcji zużyć jak najmniejszą ilość blachy?

Wzór na objętość walca to V = πr²h

Wyliczamy wysokość:








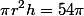
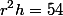
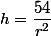
Wzór na pole powierzchni walca będzie następujący:



Przekształcamy go w taki sposób by był w postaci ilorazu:





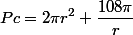
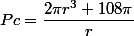
Otrzymaliśmy funkcję zależności Pola powierzchni od promienia:



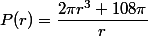
Dziedzina tej funkcji to r∈(0,+∞)

Obliczamy teraz pochodną tej funkcji:

1) Korzystamy ze wzoru na iloraz funkcji:



2) Wyliczamy pochodne z pozostałych funkcji:





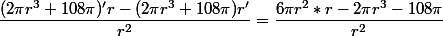
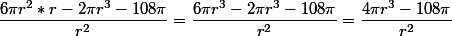
3) Zastanówmy się, kiedy pochodna będzie równa 0? Aby to zauważyć musimy ją przekształcić, tak by jeden czynnik decydował o wartości 0:



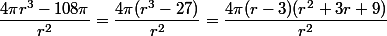
Jako że r musi być liczbą dodatnią (wynika to z dziedziny funkcji) jedyne r dla którego funkcja pochodna będzie równa 0 to r=3. Czy jest to rzeczywiście minimum tej funkcji? Aby tego dowieść trzeba zbadać okolicę punktu r=3.



Dla r<3 pochodna przyjmuje wartości ujemne a dla r>3 dodatnie. Oznacza to, że w tym miejscu jest minimum. Ponad to jest to wartość minimalna funkcji (funkcja dla argumentów większych od r=3 jest stale rosnąca a dla mniejszych stale malejąca).

Argument r=3 jest więc poszukiwanym promieniem.

Jeśli pochodna funkcji w punkcie jest równa 0 to ten punkt może być ekstremum (minimum, maksimum - nie mylić z wartością minimalną/maksymalną całej funkcji) lub punkt przegięcia.

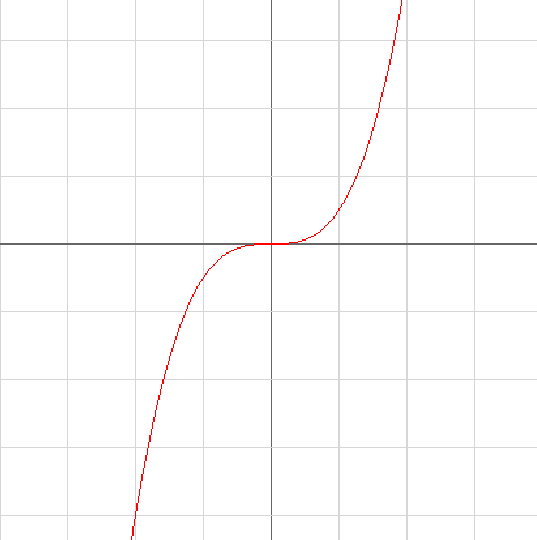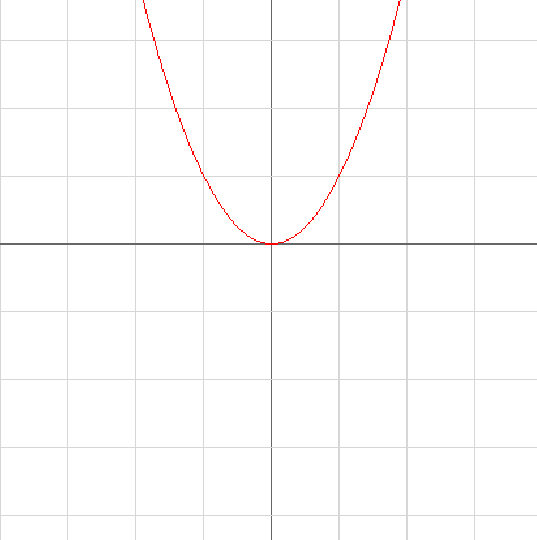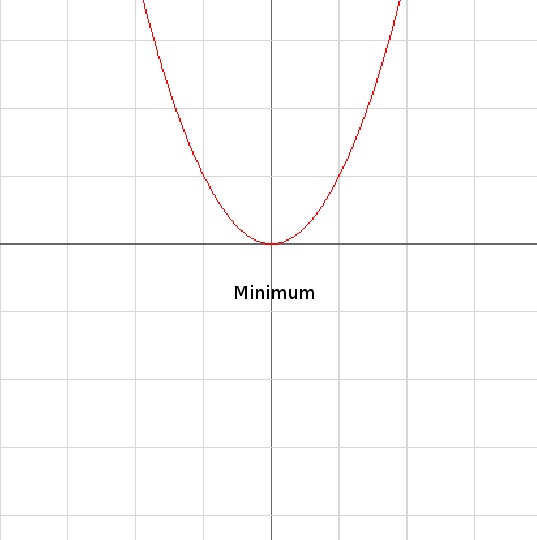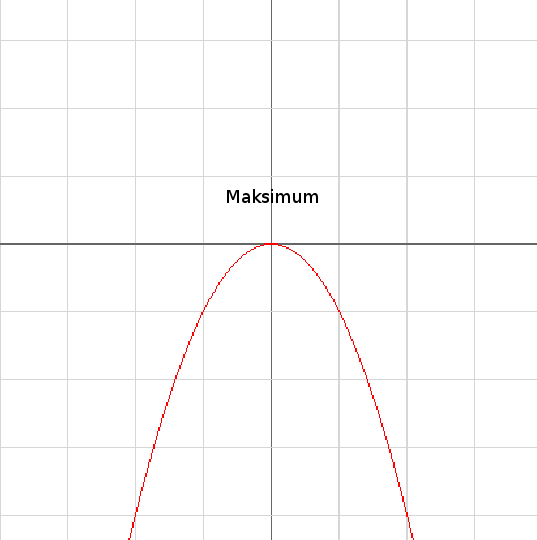
Minimum występuje gdy po obu stronach od badanego punktu funkcja ma większe wartości (po lewej stronie malejąca a po prawej rosnąca).

W przypadku maksimum jest na odwrót, natomiast punkt przegięcia wystąpi gdy po jednej i po drugiej stronie od punktu jest malejąca lub rosnąca.





Jaki promień wyszedłby gdyby walec miał objętość 16π?



Potrafisz obliczyć jaki powinien być stosunek r/h by przy jak najmniejszym polu powierzchni walca objetość była jak największa?