Zadanie: W odległości x przed wypukłą soczewką o ogniskowej równej 5cm położono przedmiot P w odległości x od soczewki (x>5). Oznaczmy literą y odległość obrazu Q tego przedmiotu od soczewki. Jaki jest wzór funkcji określającej szybkość zmiany y w zależności od x? Jaka będzie szybkość zmiany jeśli przedmiot ustawimy w odległości 55cm od soczewki, a następnie będziemy zmieniać jego położenie?

Naszkicujmy najpierw rysunek obrazujący problem:



Już na lekcjach fizyki w gimnazjum dowiedziałeś się, że ogniskową obliczamy w następujący sposób:



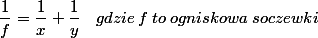
Obliczmy zależność y(x):











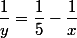
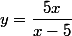
Otrzymaliśmy funkcję y(x):



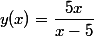
Pochodna jest miarą przyrostu funkcji. Oznacza to, że licząc pochodną w punkcie x₀ liczymy prędkość przyrostu funkcji. To dlatego w punktach będących ekstremami funkcji pochodna przyjmuje wartość 0 - funkcja tam nie jest ani rosnąca ani malejąca.

Obliczmy teraz pochodną tej funkcji. Pochodna ta będzie oznaczać szybkość zmiany y względem x:



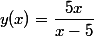
Korzystamy z wzoru na iloraz pochodnych:



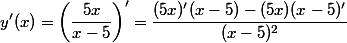
Wyliczamy pozostałe pochodne:







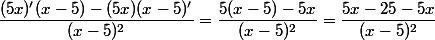
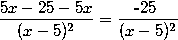
Pierwsza część zadania zrobiona. Znaleźliśmy funkcję określającą szybkość zmiany y w zależności od x.

Teraz podstawiamy dane z zadania:



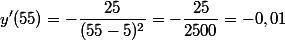
Pochodna w punkcie x=55 jest ujemna i jest równa -0,01. Oznacza to, ze jeśli z odległości 55cm od soczewki zmienimy odległość obiektu P o 1cm to odległość obrazu za soczewką od tej soczewki zmieni się o -0,01cm.

Jeśli z tego punktu przybliżymy obiekt o 5cm do soczewki to obraz Q się od niej oddali o 0,05cm. Jeśli przedmiot od soczewki oddalimy o 2cm to obraz zbliży się do niej o 0,02cm.

Co by było gdyby ogniskowa była równa 0,7? Jaka będzie szybkość zmiany y w zależności od x z 55cm? Wynik podaj w zaokrągleniu do części dziesięciotysięcznych. W obliczeniach możesz posłużyć się kalkulatorem.