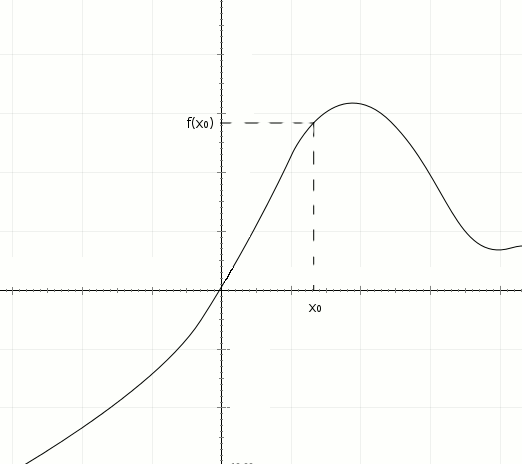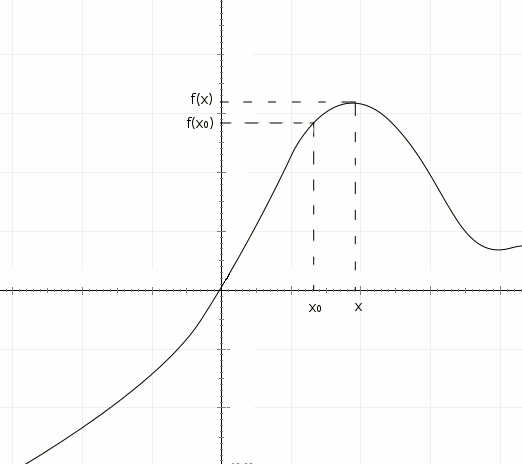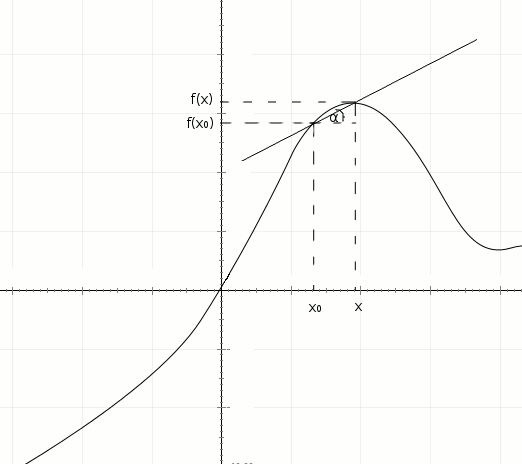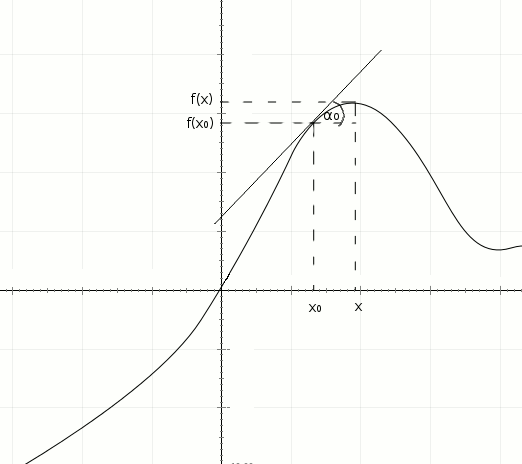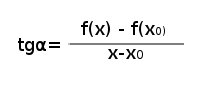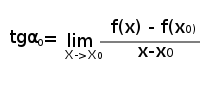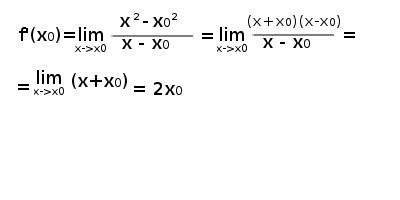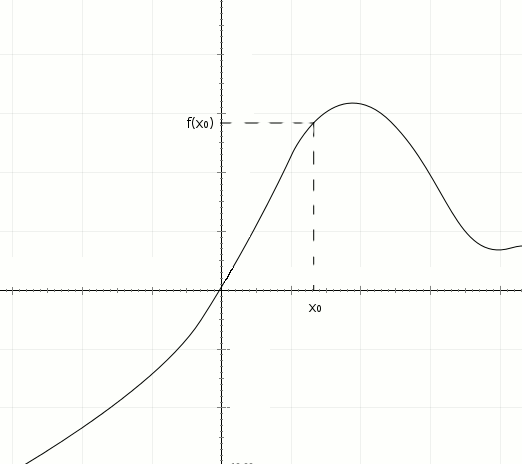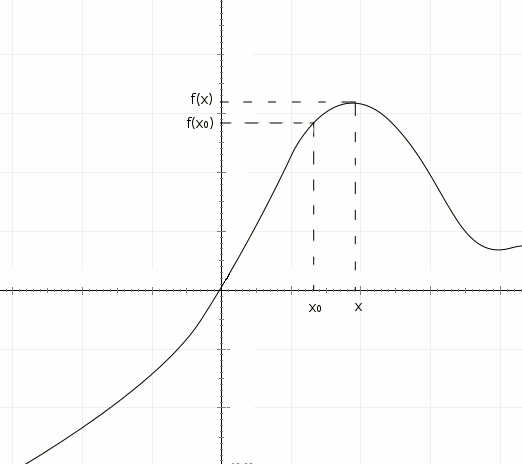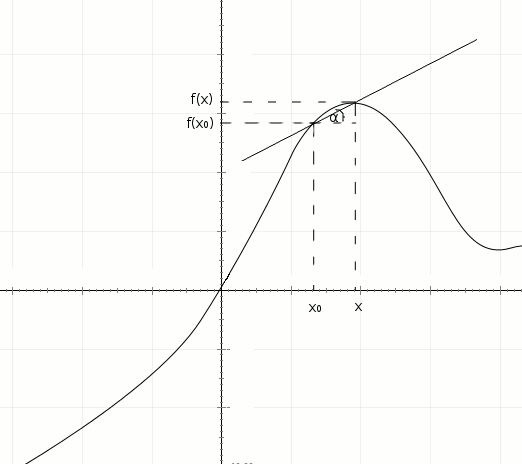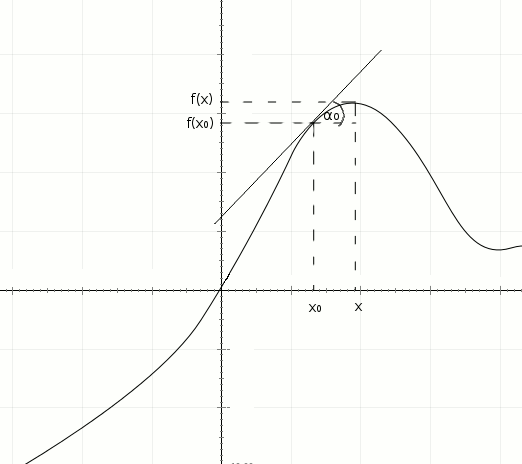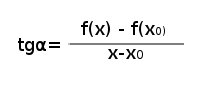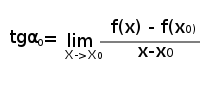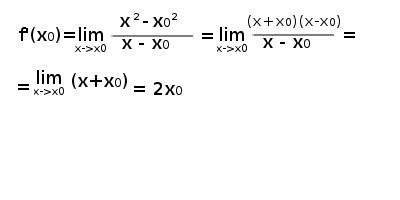Czym jest pochodna?
Z definicji pochodna jest granicą ilorazu różnicowego gdy przyrost zmiennej x (czyli inaczej ∆x) dąży do zera. Co to oznacza? Najłatwiej jest zrozumieć pochodne przyglądając się ich geometrycznej interpretacji.
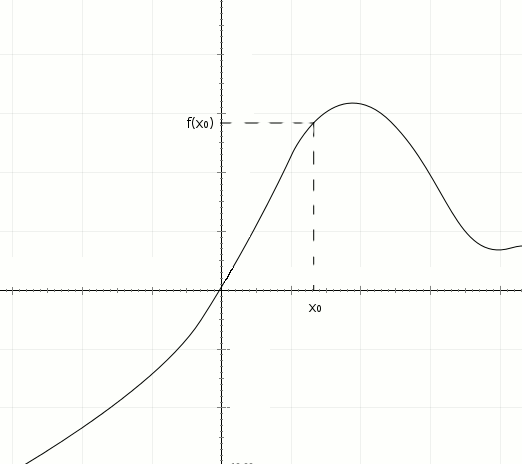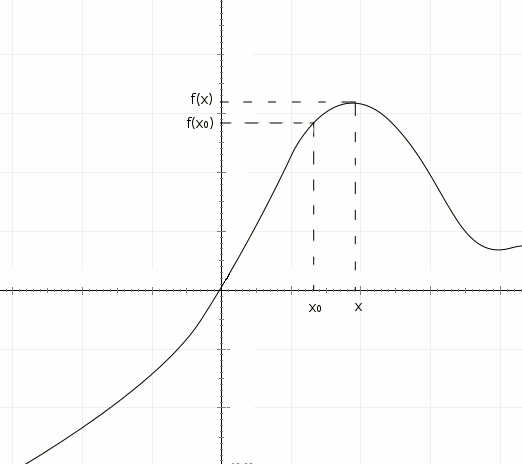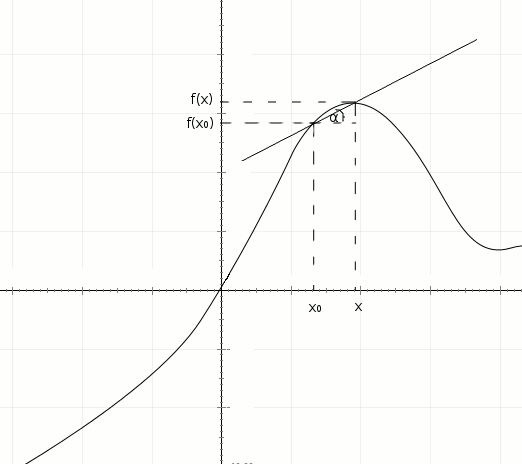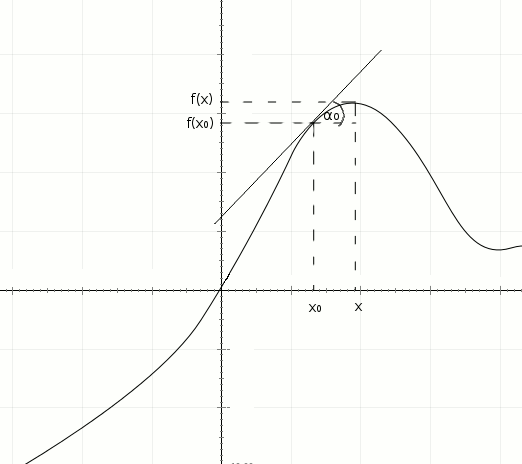
Weźmy za przykład fragment pewnej funkcji. Postępując krok po kroku dowiedzmy się czym jest pochodna:
1) Oznaczmy na funkcji punkt x0 tak jak na rysunku, następnie poprowadźmy linie pomocnicze i oznaczmy wartość jaką funkcja przyjmuje dla tego punktu.
2) Następnie podobnie oznaczmy punkt x i jego wartość, przy czym musi on być różny od x0. W celu łatwego odczytania można narysować go w większej odległości niż na animacji.
3) Jak na rysunku poprowadźmy prostą przez punkty przecięcia linii pomocniczych. Będzie ona sieczną wykresu.
4) Zaznaczmy kąt jaki utworzyła ta sieczna z osią x.
Kąt ten ma taką własność, że jego tangens(tg) jest ilorazem różnicowym:
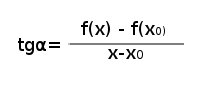
5) Poprowadźmy inną prostą, styczną do punktu przecięcia linii poprowadzonych od x0 i f(x0). Prosta ta będzie determinować granicę ilorazu różnicowego z punktu 4.
6) Powstały między osią x a prostą kąt nazwijmy α0; Jego tangens jest granicą ilorazu różnicowego z punktu 4:
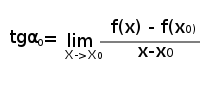
Mamy już zobrazowaną definicję pochodnej. Dla przykładu obliczmy pochodną funkcji f(x)=x2 w punkcie x0:
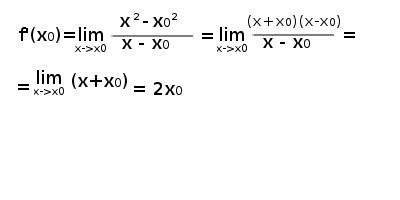 Na początku w liczniku ułamka od razu możemy zapisać wartości funkcji f(x)=x2 dla argumentów x i x0. Następnie by skrócić ułamek można było zastosować 3 wzór skróconego mnożenia. Za x podstawiamy x0 (x dąży do x0).
Na początku w liczniku ułamka od razu możemy zapisać wartości funkcji f(x)=x2 dla argumentów x i x0. Następnie by skrócić ułamek można było zastosować 3 wzór skróconego mnożenia. Za x podstawiamy x0 (x dąży do x0).
Pochodne w matematyce możemy oznaczać znakiem ' np. f'(x0). Inne oznaczenia to df/dx, Dxf albo y'.
Pochodna funkcji f(x) w punkcie x0 jest wartością jaką przyjmuje funkcja pochodna, czyli f'(x) dla argumentu x0.
Sposób obliczania funkcji z definicji wydaje się prosty, ale dlatego, że była to prosta funkcja. W celu obliczania pochodnych funkcji w praktyce stosuje się gotowe wzory:
1) (xn)' = n*xn-1
2) (√x)' = (x½)' = ½x-½ = 1 / 2√x
3) (1/x)' = (x-1)' = -1*x-2
4) (sinx)' = cosx
5) (cosx)' = -sinx
6) (tgx)'= 1/cos2x
7) (ctgx)'= 1/sin2x
8) (c)' = 0 ; c - constans [c jest wartością stałą (nie zmienną)]
9) (lnx)' = 1/x
10) (logax)' = 1/x*ln*a
Dodatkowo przydają się wzory działań na pochodnych:
11) [f(x)+g(x)]' = f'(x)+g'(x)
12) [f(x)*g(x)]' = f'(x)*g(x)+f(x)*g'(x)
13) [f(x)-g(x)]' = f'(x)-g'(x)
14) [f(x)/g(x)]' = [f'(x)*g(x)- f(x)*g'(x)]/[g(x)]2
15) [f(g)]' = f' * g'
Na stornie znajdziesz kilka przykładów zastosowań pochodnych, które pomogą Ci zrozumieć temat.