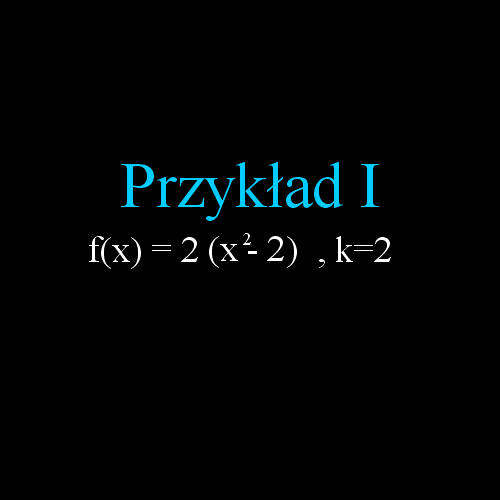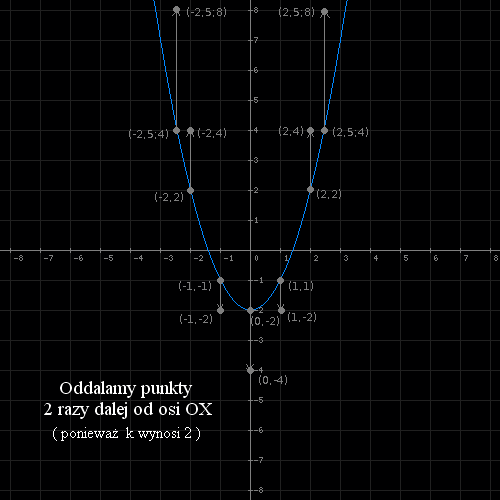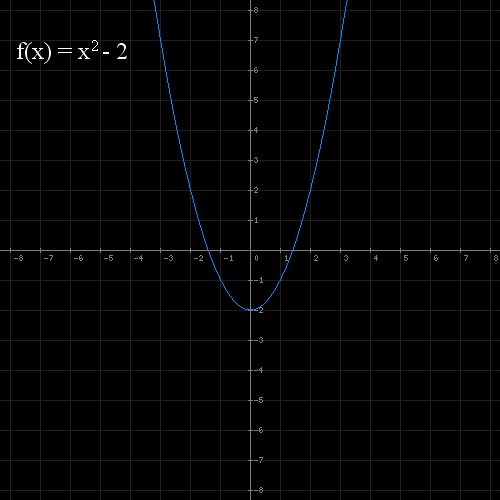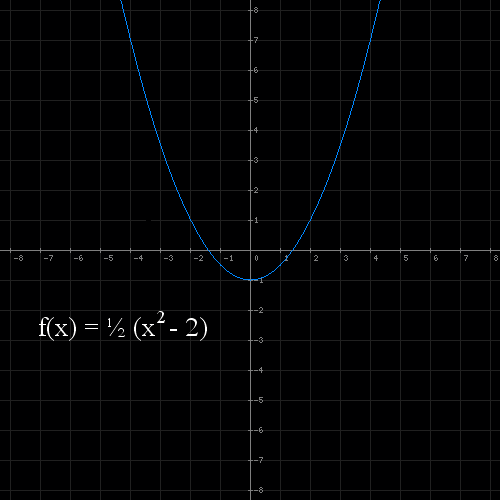Translacja jest to przesunięcie równoległe wykresu funkcji o wektor u = [ p,q ], gdzie p odpowiada za przesunięcie wykresu
w poziomie, natomiast q w pionie.

Wzór naszej funkcji przekształcony o translację będzie wyglądał tak:

f(x)=(x-p)+q.

Gdzie gdy p>0 wykres przesunie się w prawo, gdy p<0 w lewo.

Natomiast jeśli q>0 wykres przesunie się do góry, jeśli q<0 na dół.

pokażmy to na przykładach

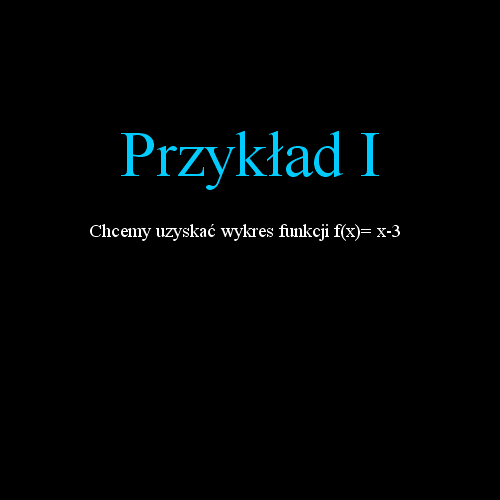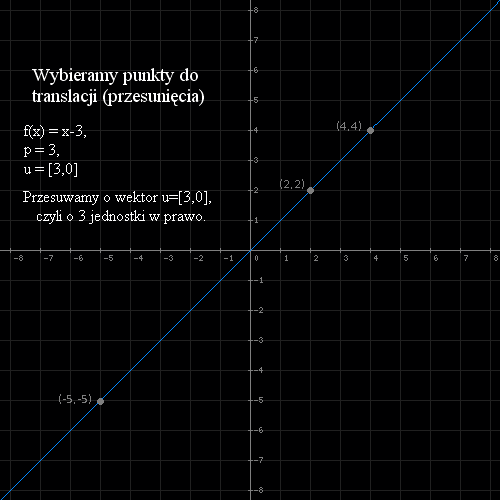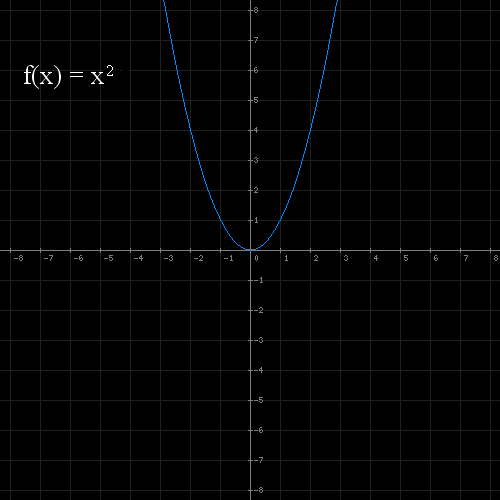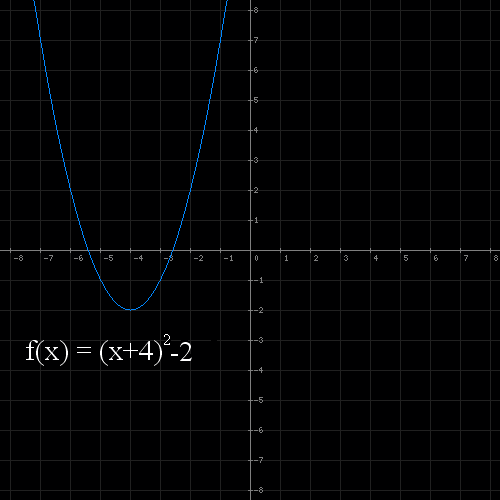
1) Symetria osiowa względem osi OX:    -f(x)

W tym przypadku naszą funkcję musimy "odbić" względem osi OX.

Mówiąc prościej - to co znajduje się nad osią OX przenosimy pod oś, to co znajduje się pod osią przenosimy nad oś OX (oczywiście o tyle samo jednostek).

Podczas tej symetrii współrzędne Y punktów zmieniają swoje znaki na przeciwne np.: punkt (3,3) zmienia się w punkt (3,-3).

2) Symetria osiowa względem osi OY:   f(-x)

W tym przypadku podobnie jak w poprzednim naszą funkcję musimy "odbić" względem osi, tym razem OY.

To co znajduje się po lewej/prawej stronie osi OY przenosimy na stronę przeciwną (oczywiście o tyle samo jednostek).

Podczas tej symetrii współrzędne X punktów zmieniają swoje znaki na przeciwne np.: punkt (5,-3) zmienia się w punkt (-5,-3).

3) Symetria osiowa względem początku układu współrzędnych:    -f(-x)

W tym przypadku podobnie jak w poprzednich naszą funkcję musimy "odbić", tym razem względem obu osi na raz.

Wykres funkcji przenosimy symetrycznie względem początku układu współrzędnych O(0,0)

Podczas tego przekształcenia współrzędne funkcji zmieniają swoje znaki na przeciwne np.: punkt (-5,2) zmienia swoje współrzędne na (5,-2).

1) Nakładanie wartości bezwzględnej na całą funkcję:   |f(x)|

W tym przypadku część wykresu znajdującą się pod osią X "odbijamy" ponad oś.

2) Nakładanie wartości bezwzględnej na zmienną x:    f(|x|)

W tym przypadku usuwamy część wykresu znajdującą się po lewej stronie osi OY. Natomiast prawą stronę odbijamy symetrycznie na lewą względem osi OY.

1) Względem osi OX o skali k

Mówiąć najprościej jest to rozciągnięcie lub ściśnięcie wykresu funkcji wzdłuż osi OX o skalę k.

Wzór ogólny:

y = f(k*x)

(nasza skala dotyczy samego x)

A więc jeśli nasza skala będzie większa od 1 ( k>1 ) to wykres ściśnie się k razy wzdłuż osi OX,

natomiast jeśli skala będzie większa od 0 i mniejsza od 1 to wykres rozciągnie się k razy wzdłuż osi OX.

pokażmy to na przykładach

2) Względem osi OY o skali k

Jest to rozciągnięcie lub ściśnięcie wykresu funkcji wzdłuż osi OY o skalę k.

Wzór ogólny:

y = k*f(x)

(nasza skala dotyczy całego wyrażenia)

A więc jeśli nasza skala będzie większa od 1 ( k>1 ) to wykres rozciągnie się k razy wzdłuż osi OY,

natomiast jeśli skala będzie większa od 0 i mniejsza od 1 to wykres ściśnie się k razy wzdłuż osi OY.