Do góry
Wstęp Funkcja i jej własności Przekształcanie wykresów funkcji Rysowanie wykresów funkcji - przykłady

Rysowanie wykresów funkcji - przykłady

Przykład 1 :     f(x) = 2x + 3

Mamy narysować funkcję liniową f(x) = 2x + 3

W przypadku prostych funkcji liniowych po prostu:

  1. Wybieramy kilka punktów z dziedziny
  2. Obliczamy odpowiednie dla nich wartości funkcji
  3. Rysujemy wykres funkcji

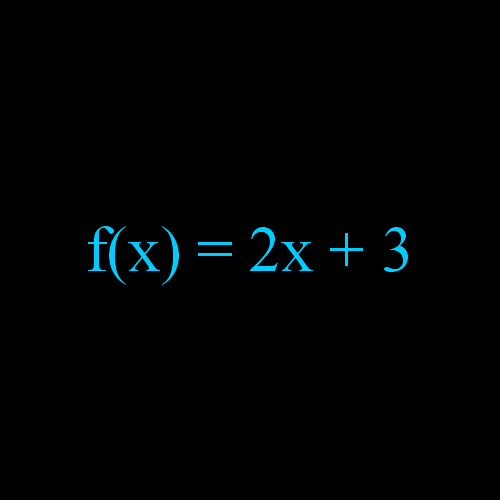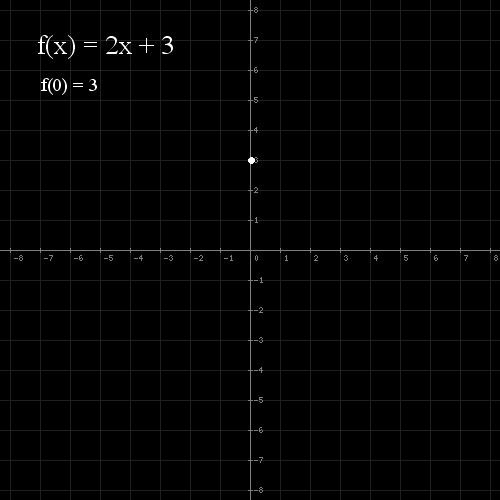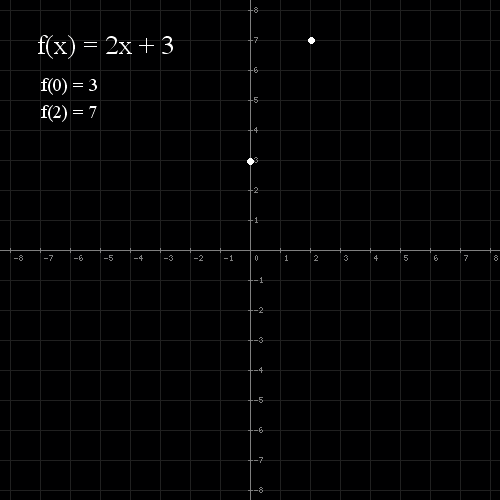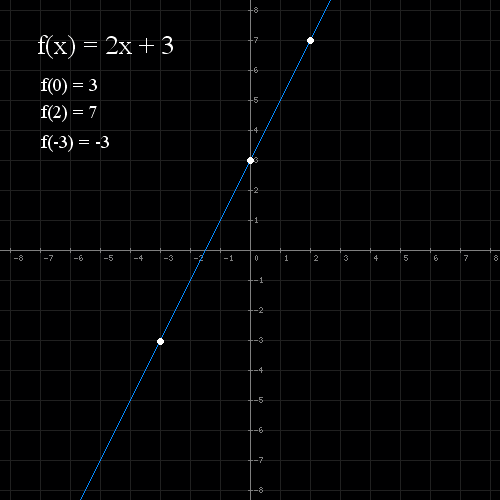
Przykład 2 :     f(x) = ( x - 3 ) 2 - 4

Mamy narysować funkcję kwadratową f(x) = ( x - 3 ) 2 - 4

W przypadku tej funkcji mamy podany wzór kanoniczny (wzór z którego w łatwy sposób możemy odczytac przesunięcie funkcji):

  1. Rysujemy wykres f(x) = x 2

  2. Translacja: p = 3, q = -4, u=[3 , -4]

  3. Przesuwamy wyres funkcji o wektor przesunięcia u=[3 , -4]

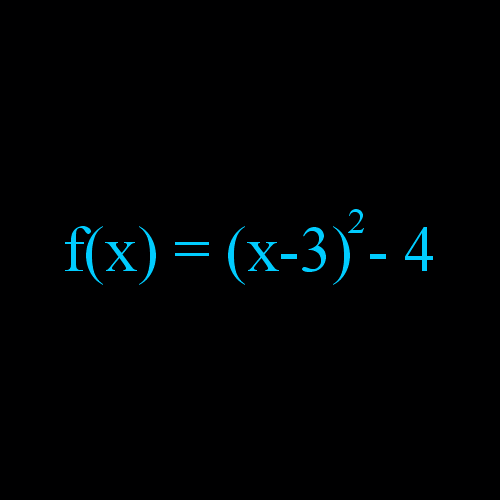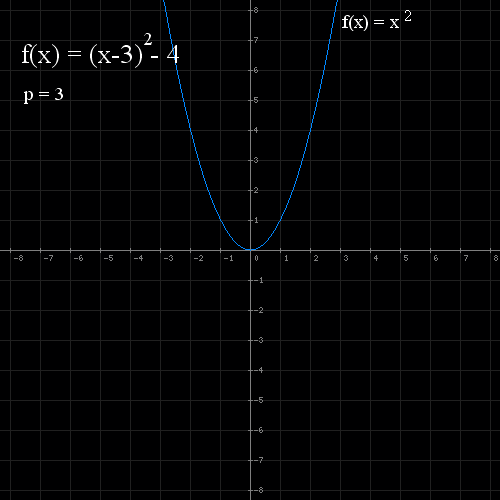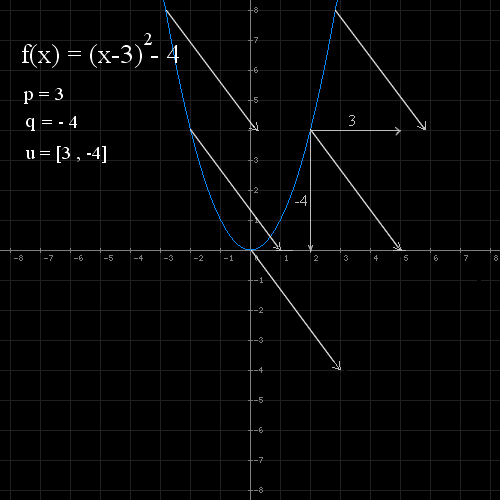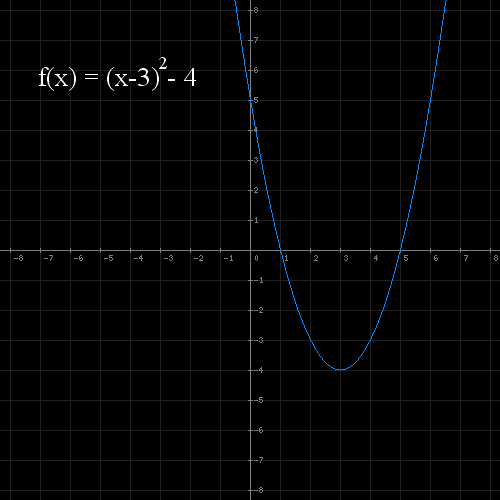
Przykład 3 :     f(x) = | x - 4 | - 3

Mamy narysować funkcję f(x) = | x - 4 | - 3

Kolejność przekształceń:

  1. Rysujemy wykres funkcji f(x) = x - 4    (jeśli nie wiesz jak to zrobić patrz na przykład pierwszy)

  2. Część wykresy leżącą pod osią OX odbijamy symetrycznie względem osi OX ( wartość bezwzględna )

  3. Przesuwamy wyres funkcji o 3 jednostki w dół

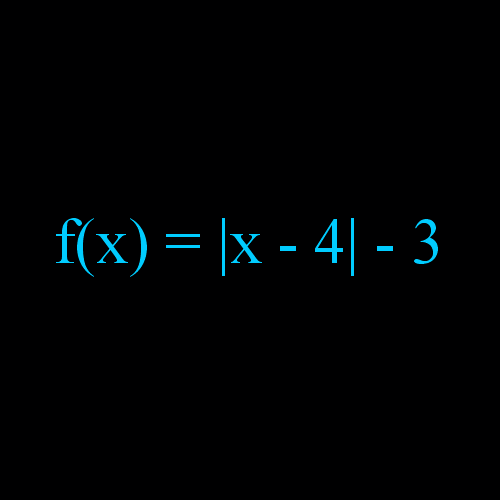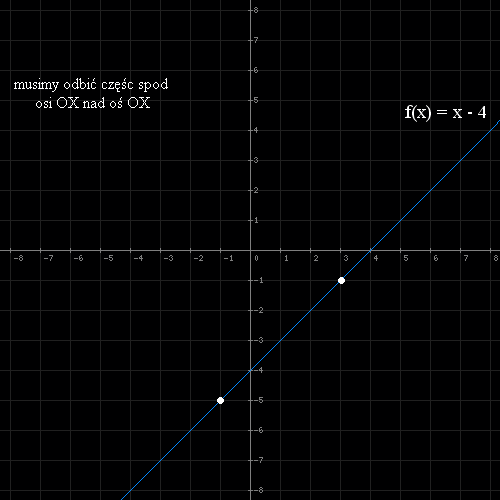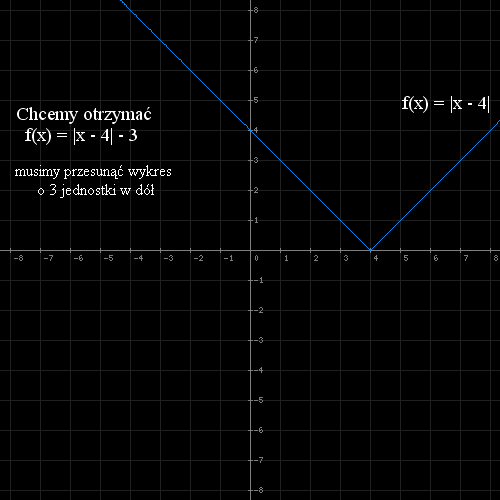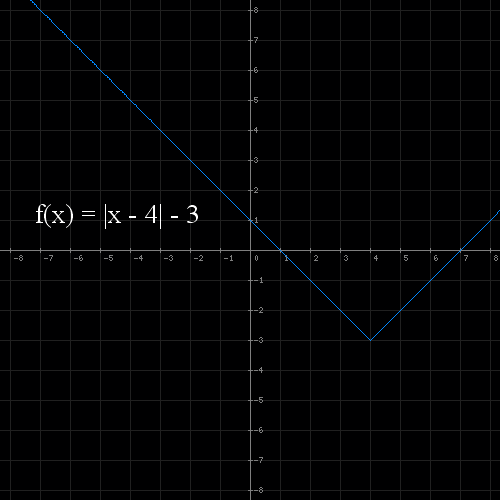
Przykład 4 :     f(x) = - 2 ((x+3) 2 - 2)

Mamy narysować funkcję f(x) = - 2 ((x+3) 2 - 2)

Kolejność przekształceń:

  1. Rysujemy wykres funkcji f(x) = x 2

  2. Translacja: przesuwamy go o wektor u=[-3, -2] i rysujemy wykres f(x) = (x+3) 2 - 2

  3. Symetria względem osi OX :  -f(x) - otrzymujemy wykres funkcji f(x) = - ((x+3) 2 - 2)

  4. Teraz musimy rozciągnąć wykres 2 razy wzdłuż osi OY - otrzymujemy wykres f(x) = - 2 ((x+3) 2 - 2)

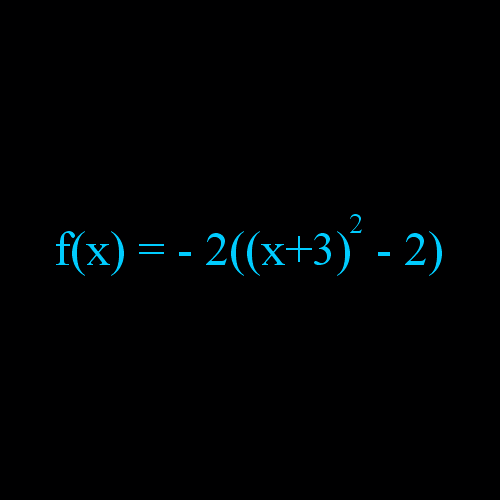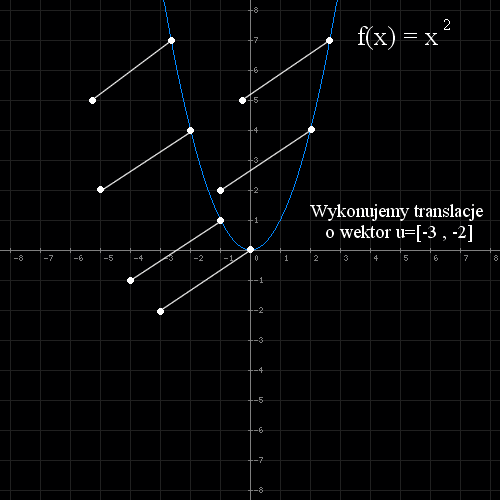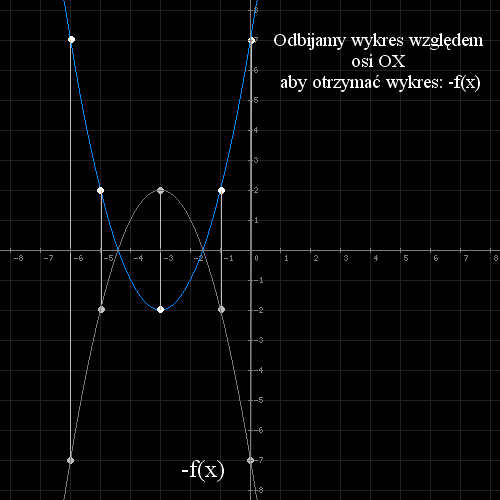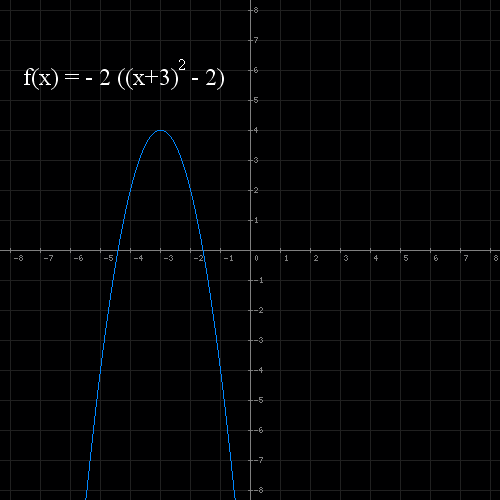
Przykład 5 :     f(x) = ( |x| - 2 ) 2 - 3

Mamy narysować funkcję f(x) = ( |x| - 2 ) 2 - 3

Kolejność przekształceń:

  1. Rysujemy wykres funkcji f(x) = x 2

  2. Translacja: przesuwamy go o wektor u=[2, -3] i rysujemy wykres f(x) = (x-2) 2 - 3

  3. Wartość bezwzględna nałożona na x :  f(|x|) - otrzymujemy wykres f(x) = (|x|-2) 2 - 3

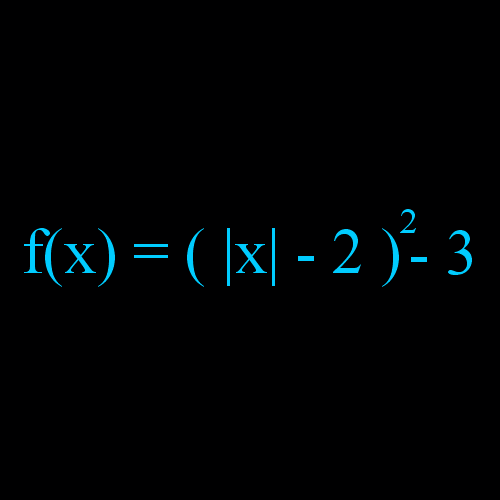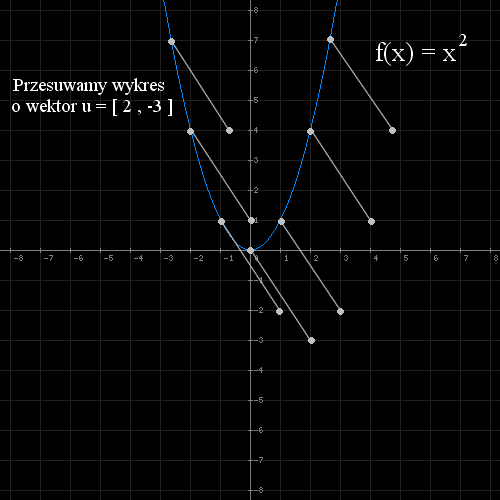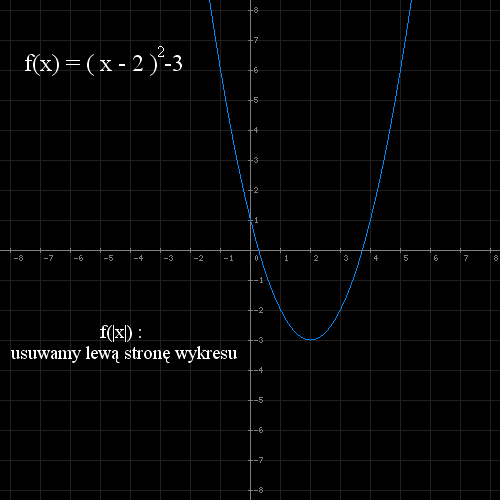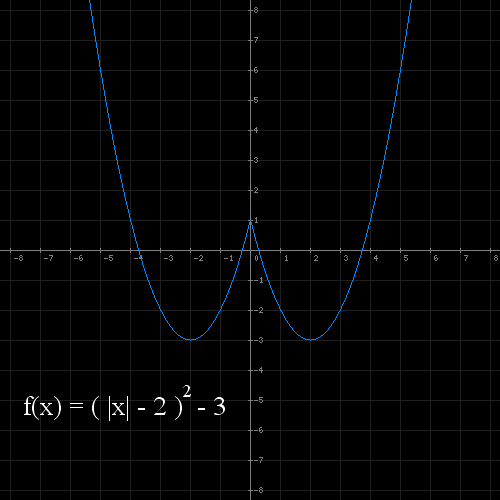
Przykład 6 :     f(x) = - (| - ½ x + 1 | + 3)

Mamy narysować funkcję f(x) = - (| - ½ x + 1 | + 3)

Kolejność przekształceń:

  1. Rysujemy wykres funkcji f(x) = x , przesunięty o translację u = [1 , 0]

  2. Powinowactwo prostokątne względem osi OX, k wynosi 1/2 - wykres rozciągnie się 2 razy wzdłuż osi OX

  3. Na powstałą funkcję nakładamy wartość bezwzględną - odbijamy to co pod osią OX nad oś OX:    | f(x) |

  4. Powstałą funkcję przesuwamy o 3 jednostki w górę

  5. Powstałą funkcję przekształcamy o symetrię względem początku układu współrzędnych ( punktu O(0,0) ):    -f(-x)

dawid0000@gmail.com
Wstęp Funkcja i jej własności Przekształcanie wykresów funkcji Rysowanie wykresów funkcji - przykłady Stronę zrobił Dawid Jagieła