Funkcja określona na zbiorze X o wartościach w zbiorze Y jest to przyporządkowanie
każdemu elementowi ze zbioru X dokładnie jednego elementu ze zbioru Y.

Przykładem funkcji jest przyporządkowanie uczniom numerów w dzienniku. Uczniowie tworzą zbiór X (dziedzinę) natomiast numery zbiór Y (wartości funkcji). Każdy uczeń otrzymuje dokładnie jeden numer.

Dane przyporządkowanie jest funkcją, jeśli danemu elementowi z jednego zbioru przyporządkowuje dokładnie jeden element ze zbioru drugiego.

(Nie jest błędem, gdy dwóm lub kilku różnym argumentom funkcja przyporządkowuje takie same wartości. Może się tak zdarzyć na przykład w przypadku funkcji kwadratowej.)

Zbiór X nazywamy dziedziną funkcji i oznaczamy go jako D, elementy dziedziny nazywamy argumentami.

Zbiór Y nazywamy zbiorem wartości, a jego elementy wartościami.

• tabelki:

  
  
  

• grafu:

  
  
  

• wykresu:

  
  
  

• wzoru:

  
  

  f(x) = 2x + 5

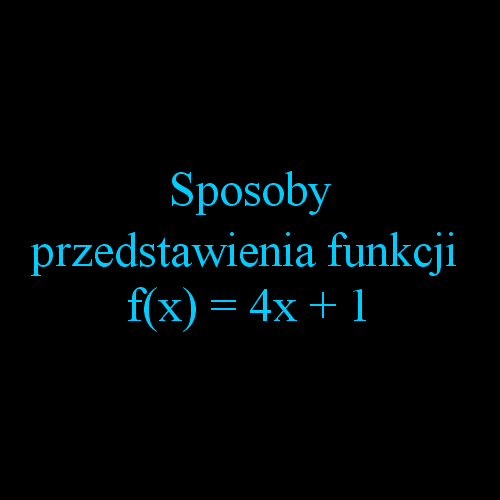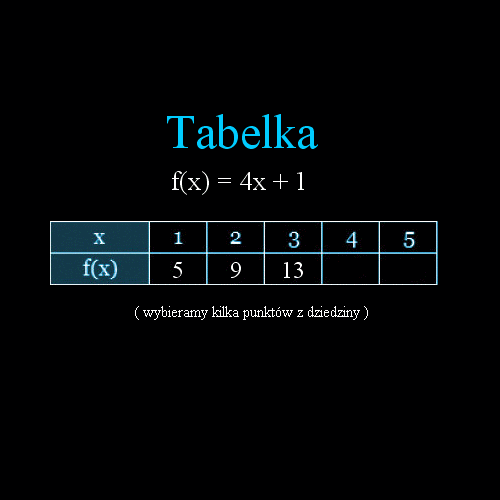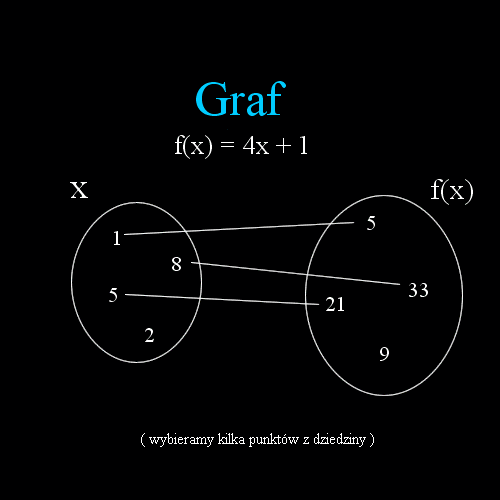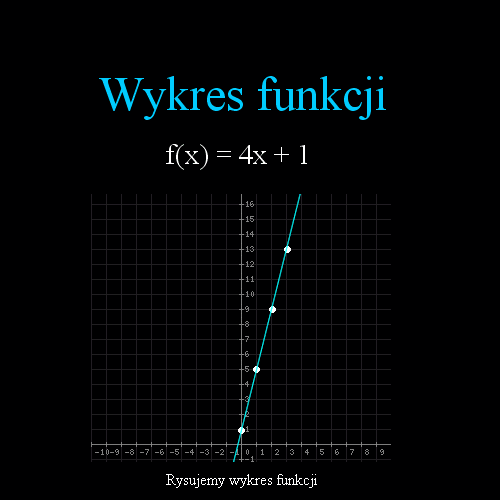
Miejscem zerowym funkcji y=f(x) nazywamy każdą wartość argumentu x, dla której wartość funkcji równa jest zero [ f(x) = 0 ].

Miejsce zerowe jest to miejsce przecięcia się wykresu z osią OX.

Funkcja jest różnowartościowa jeśli nie ma takich dwóch ( ani więcej ) argumentów dla których funkcja przyjmuje taką samą wartość.

Aby zbadać czy funkcja jest różnowartościowa należy sprawdzić czy każdej parze różnych argumentów przyporządkowuje różne wartości funkcji, tzn.

Funkcja jest okresowa jeżeli jej wykres da się podzielić na nieskończenie wiele takich samych części.

Okres funkcji, jest to długość części na jakie został podzielony wykres.

Funkcjami okresowymi są np.: sin(x), cos(x), tg(x), ctg(x), x-[x] (cecha z x).

1) Funkcja jest parzysta jeśli dziedzina funkcji jest symetryczna względem zera oraz dla dowolnych przeciwnych argumentów jej wartość wynosi tyle samo (wykres funkcji jest symetryczny względem osi OY) :

f(x) = f(-x)

Mówiąc prościej - lewa strona wykresu jest odbiciem prawej.

2) Funkcja jest nieparzysta jeśli dziedzina funkcji jest symetryczna względem zera oraz dla dowolnych przeciwnych argumentów ich wartość też jest przeciwna (funkcja jest symetryczna względem początku układu współrzędnych):

- f(x) = f(-x)

Mówiąc prościej - lewa strona wykresu jest odwróconym odbiciem prawej.