banner




Grafy eulerowskie

Ścieżka Eulera

W okolicy powstało kilka nowych szlaków rowerowych. Monika bardzo lubi jeździć na rowerze, a przy okazji zobaczy kilka nowych miejsc. Jako że przejeżdżanie kilka razy tą samą drogą jest nudne, postanowiła wymyślić sobie taką trasę, aby nie przejeżdżać żadną z tych dróg więcej niż raz, ale aby każdą z wybranych udało jej się przejechać. Z którego miejsca powinna zacząć i w którym miejscu skończyć, aby to było możliwe?

Zbudujmy graf. Wierzchołkami będą miejsca, w których przecinają się szlaki. W grafie chcemy znaleźć ścieżkę Eulera. Jest to ścieżka, która przechodzi przez wszystkie krawędzie w grafie dokładnie raz.
Poniżej graf, w którym istnieje ścieżka Eulera oraz podana przykładowa taka ścieżka:
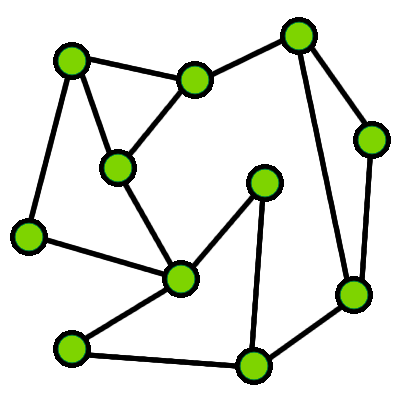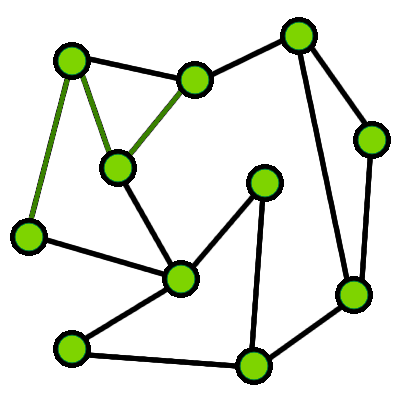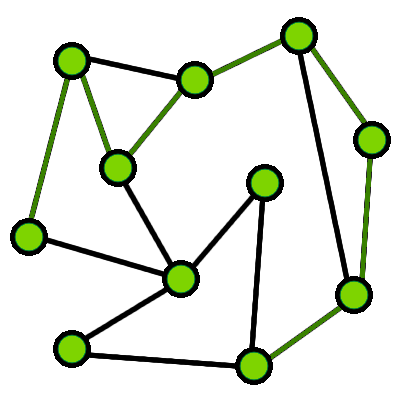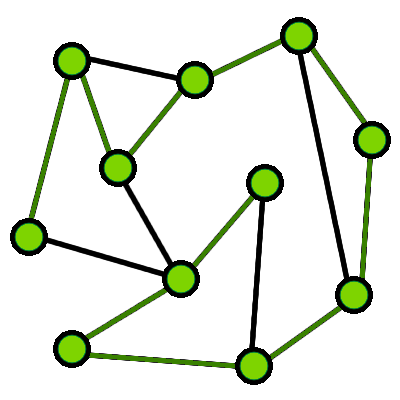
sciezka eulera
Graf, w którym istnieje ścieżka Hamiltona (a nie istnieje cykl Hamiltona) nazywamy półeulerowskimi.

Cykl Eulera

Z okazji Dnia Ziemi Monika wraz ze swoją klasą chcą przejść wzdłuż wszystkich ulic miasta i pozbierać zalegające śmieci. Nie mogą się rozdzielić, nie ma też potrzeby przechodzenia drugi raz ulicą, która jest już wysprzątana. Mapkę miasta rozrysowali w formie grafu. Czy możliwe jest zaplanowanie takiej trasy, aby przejść każdą ulicą dokładnie raz? Pamiętaj, że startują ze szkoły i do szkoły muszą wrócić.

Znowu mamy problem podobny jak wyżej, z tym, że chcemy zakończyć naszą podróż w tym samym miejscu co skończyliśmy. Dokładniej, to chcemy wyznaczyć cykl Eulera. Do rozwiązanie tego zagadnienia w informatyce służy nam algorytm Fleury'ego.
Zobaczmy sobie dla przykładu jak może wyglądać taki cykl w poniższym grafie:
cykl eulera

Graf, w którym istnieje cykl Eulera, nazywamy grafem eulerowskim.


Created by Monika Ciosek