|
|||
|
|||
Rodzaje grafów
|
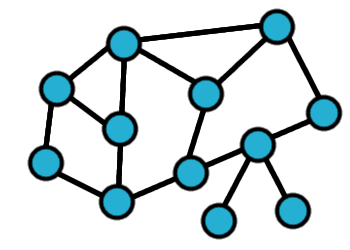
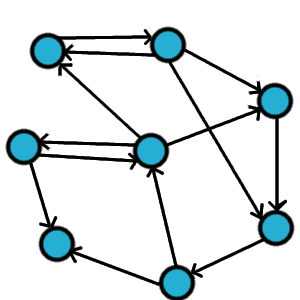
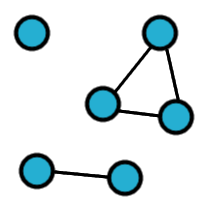
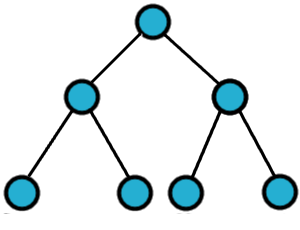
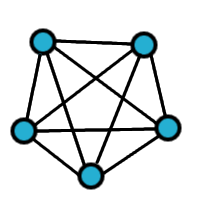
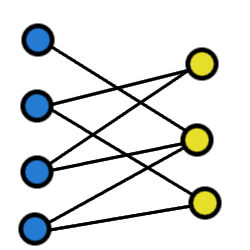
Rodzajów grafów jest bardzo wiele i nie będziemy ich wszystkich omawiać. Powiemy tylko o tych podstawowych i tych, które przydadzą nam się w późniejszych rozważaniach. GRAF NIESKIEROWANY Grafy możemy klasyfikować biorąc pod uwagę różne kryteria. Istnieją grafy skierowane i nieskierowane. Nieskierowane to takie, jakie poznaliśmy na początku, czyli jest to zbiór wierzchołków i krawędzi, wierzchołki należące do krawędzi są po prostu jej końcami. GRAF SKIEROWANY Natomiast w grafie skierownym krawędzie oznaczane strzałkami pokazują nam konkretny kierunek, w którym możemy poruszać się po grafie. GRAF SPÓJNY I NIESPÓJNY Następnie spójność - graf jest spójny jeżeli dla każdej pary wierzchołków istnieje ścieżka, która je łączy. Zazwyczaj w naszych rozważaniach będą nas interesować grafy spójne, ale zobaczmy przykład grafu niespójnego po lewej: DRZEWO I DAG Grafy możemy sklasyfikować pod względem istnienia w nich cykli - graf który nie zawiera cykli zwany jest grafem acyklicznym. Jeśli graf nie zawiera cykli, jest spójny i nieskierowany to taki graf nazywamy drzewem. Drzewa możemy dodatkowo klasyfikować, są też bardzo użyteczne w rozwiązywaniu wielu problemów algorytmicznych, dlatego warto je zapamiętać. Graf acykliczny skierowany jest nazywany dagiem, graf musi być dagiem, aby możliwe było posortowanie go topologicznie. GRAF PEŁNY Graf pełny - to taki graf prosty, w którym dla każdej pary wierzchołków istnieje krawędź je łącząca. GRAF DWUDZIELNY W matematyce często spotykanymi grafami są także grafy dwudzielne - jego zbiór wierzchołków można podzielić na dwa rozłączne zbiory tak, że krawędzie nie łączą wierzchołków tego samego zbioru. Jeśli pomiędzy wszystkimi parami wierzchołków należących do różnych zbiorów istnieje krawędź to taki graf nazywamy grafem pełnym dwudzielnym. GRAF HAMILTONOWSKI I EULEROWSKI Omówimy jeszcze grafy hamiltonowskie i eulerowskie, ale o nich szerzej na kolejnych stronach. Na następnych stronach poznamy zastosowania grafów w rozwiązywaniu ciekawych zadań. |
||
Created by Monika Ciosek |
|||