Przed Moniką bardzo pracowity dzień. Ma do zrobienia wiele zadań, jednak aby wykonać pewne zadanie musi często wykonać jakieś inne np. najpierw musi pójść do sklepu kupić składniki na ciasto, a dopiero potem może je upiec. Pomóż Monice ustalić kolejność w jakiej powinna wykonywać zadania przeznaczone na ten dzień.

Mamy dany graf skierowany, acykliczny, tzw. dag. To, co chcemy zrobić w tym zadaniu to ustalić kolejność topologiczną zadań  - wierzchołków grafu. W teorii grafów sortowanie topologiczne skierowanego grafu acyklicznego to liniowe uporządkowanie wierzchołków, w którym jeśli istnieje krawędź skierowana prowadząca od wierzchołka do , to znajdzie się przed wierzchołkiem . Innymi słowy, każdy wierzchołek poprzedza wszystkie te wierzchołki, do których prowadzą wychodzące od niego krawędzie.
Do sortowania topologicznego wykorzystuje się znany nam już DFS.
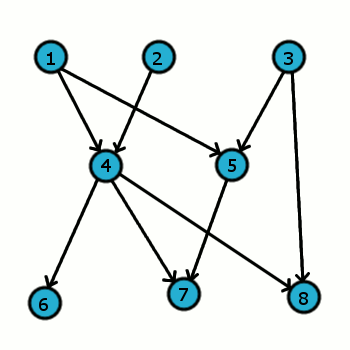
Dla powyższego grafu możliwe są kolejności:

1, 2, 3, 4, 5, 6, 8, 7

1, 2, 4, 6, 3, 8, 5, 7

3, 1, 5, 2, 4, 8, 7, 6

I to by było na tyle, czego się nauczymy na tej stronie. O grafach można mówić jeszcze długo i szeroko, jest całe mnóstwo grafów, o których nawet nie wspomniałam na tej stronie i jeszcze więcej problemów, które ich dotyczą. Zachęcam do tego, aby zainteresować się tym bardziej, gdyż jest to wyjątkowo ciekawy dział matematyki i informatyki :).