Monika wybiera się do dużego miasta odwiedzić znajomych. Tylko że każdy z nich mieszka w innym miejscu! Zaznaczyła je wszystkie na mapce wraz z dogodnymi dojazdami. Żadnego ze znajomych nie chce pominąć, gdyż mógłby się obrazić, koło żadnego z nich nie chce przejeżdżać też więcej niż jeden raz, gdyż znowu zaprosiłby ją do siebie i nie zdążyłaby odwiedzić innych. Od którego ze znajomych powinna zacząć i na którym skończyć odwiedziny, aby każdego udało się odwiedzić dokładnie raz?

Zbudujmy graf. Wierzchołkami będą miejsca, w których mieszkają znajomi, a krawędzie możliwymi dojazdami. W grafie chcemy znaleźć ścieżkę Hamiltona. Jest to ścieżka, która przechodzi przez wszystkie wierzchołki w grafie dokładnie raz. Oczywiście nie w każdym grafie istnieje taka ścieżka, sprawdzenie tego czy ona istnieje i wyznaczenie przez które przechodzi jest problemem algorytmicznym NP-zupełnym, co oznacza, że nie istnieją efektywne algorytmy odpowiadające na pytanie czy taka ścieżka w grafie istnieje czy nie.

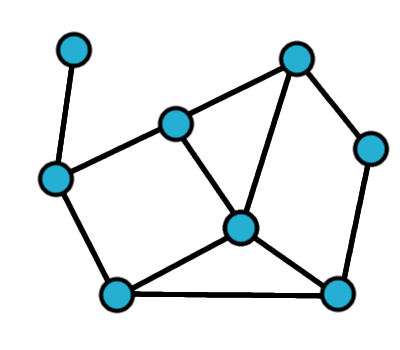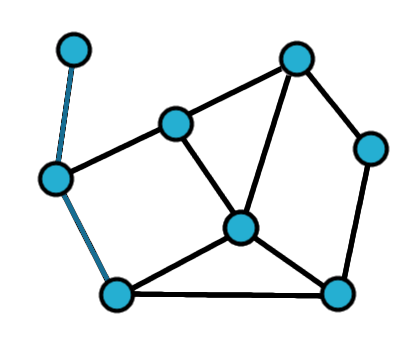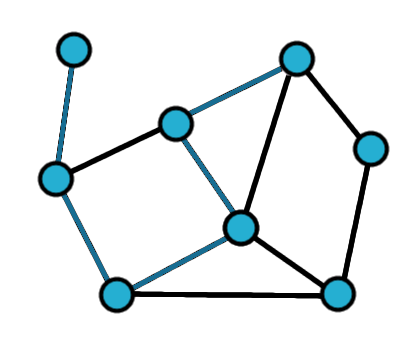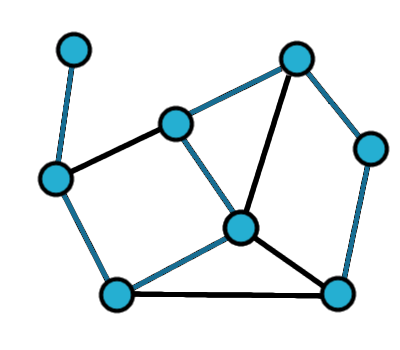
Graf, w którym istnieje ścieżka Hamiltona (a nie istnieje cykl Hamiltona) nazywamy półhamilotnowskimi.