Przeszukiwania
w grafach
Przeszukiwania w grafach są bardziej informatycznym
punktem widzenia na grafy, jednak te dwa najprostsze
sposoby przeszukiwań grafów warto znać, gdyż są bardzo
użyteczne i pomagają rozwiązać niektóre problemy.
BFS (przeszukiwanie wszerz)
BFS należy do tych najprostszych
algorytmów przeszukiwania grafu. Polega na tym, że
przechodzenie zaczynamy z zadanego wierzchołka i
odwiedzamy wszystkie z niego osiągalne, następnie
osiągalne z każdego z tych odwiedzonych itd. Wynikiem
działania algorytmu jest drzewo o korzeniu w zadanym
wierzchołku, zawierające wszystkie wierzchołki z
których prowadzi droga z tego wierzchołka startowego.
Algorytm działa prawidłowo dla grafów zarówno
skierowanych jak i nieskierowanych, ale nie ważonych!
Ten prosty algorytm ma bardzo ważne i praktyczne
zastosowania:
- znajdowanie najkrótszych ścieżek między dwoma
wierzchołkami,
- znajdowanie wszystkich połączonych węzłów w grafie,
- sprawdzanie czy graf jest dwudzielny.
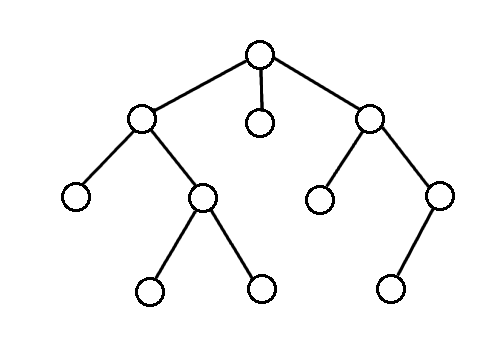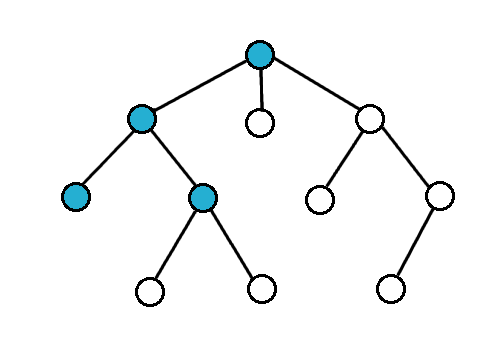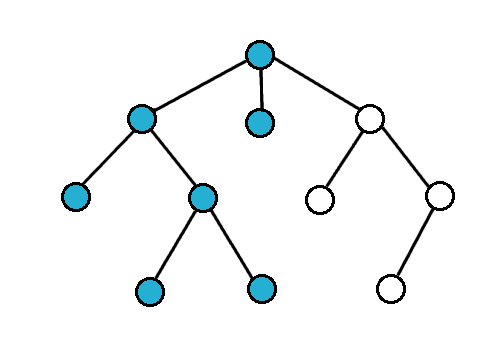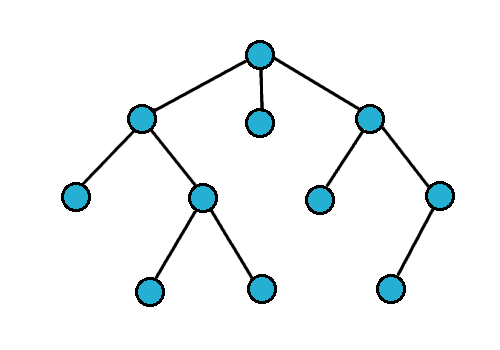
Poniżej pokazuję jak działa algorytm:
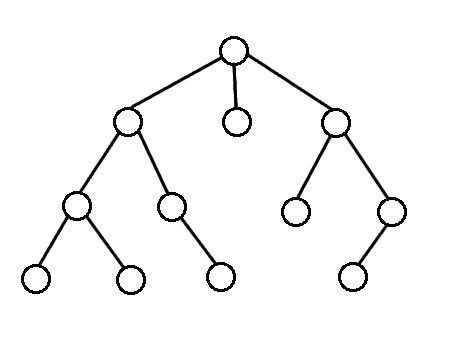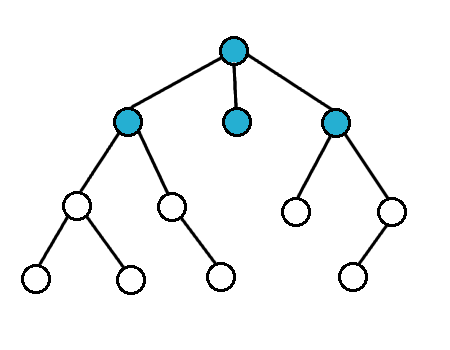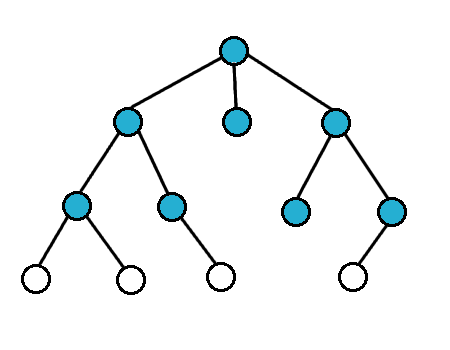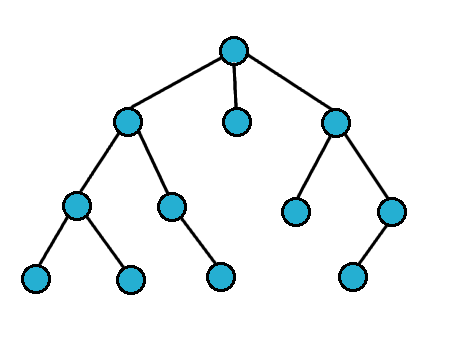
DFS (przeszukiwanie w głąb)
Przeszukiwanie w głąb polega na
badaniu wszystkich krawędzi wychodzących z podanego
wierzchołka. Po zbadaniu wszystkich krawędzi
wychodzących z danego wierzchołka algorytm powraca do
wierzchołka, z którego dany wierzchołek został
odwiedzony.
DFS ma również kilka ważnych zastosowań:
- badanie spójności grafu,
- do sortowania topologicznego,
- przy wyznaczaniu silnie spójnych składowych.
Brzmi może odrobinę zagmatwanie, obejrzyjmy zatem
animację, która zilustruje nam działanie tego
algorytmu: