Krzywe b-sklejane
Modelowanie figur o skomplikowanym kształcie wymagałoby użycia krzywych Béziera wysokiego stopnia, co sprawiałoby, oprócz niewygody użytkowania, różne kłopoty implementacyjne.
Dlatego stosuje się krzywe kawałkami wielomianowe w reprezentacji b-sklejanej, która jest uogólnieniem reprezentacji wielomianowych krzywych Béziera.
Krzywa b-sklejana jest określana przez podanie stopnia sklejanych wielomianów n, ciągu m + 1 węzłów u0, ..., un (ciąg ten powinien być niemalejący, a ponadto m powinno być większe od 2n), oraz m - n punktów kontrolnych p0, ..., pm-n-1.
Ciąg un węzłów krzywej dzieli przedział t ∈ [0,1] na podprzedziały, na których definiowane są poszczególne krzywe wielomianowe.
Wzór będący definicją ma postać:
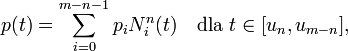
Gdzie
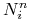jest unormowaną funkcją b-sklejaną stopnia n, którą można przedstawić za pomocą rekurencyjnego wzoru Mansfielda-de-Boora-Coxa, będącego podstawą algorytmu de Boora: 
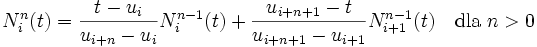
Poniżej przykładowa wielomianowa jednorodna krzywa b-sklejana:
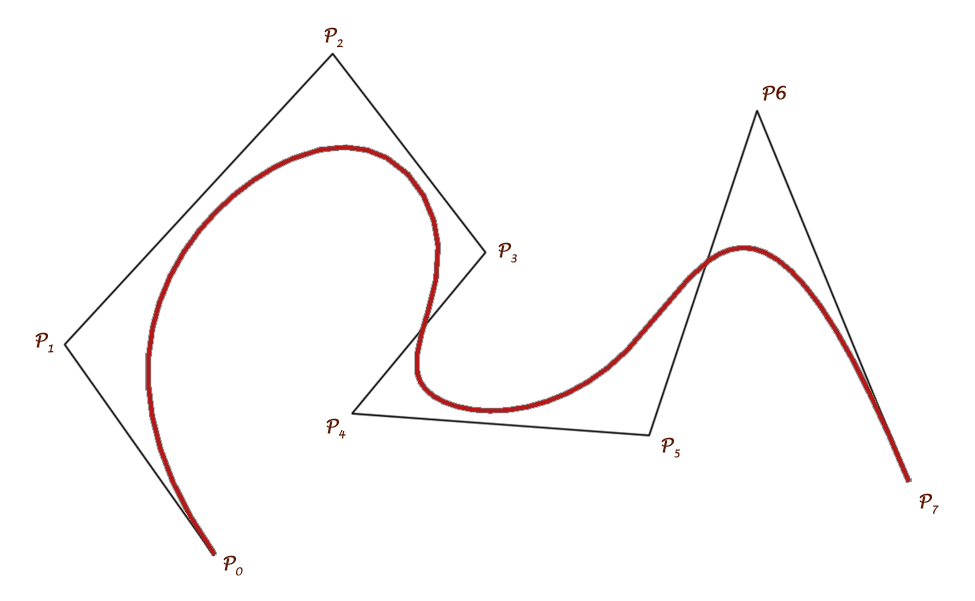
Jeśli węzły dzielą przedział t ∈ [0,1] równomiernie, krzywa jest określana jako uniform, co można tłumaczyć jako (krzywa) jednorodna/równomierna.
Jeśli węzły dzielą przedział nierównomiernie to krzywa w j.ang. jest nazywna non-uniform, czyli krzywa jest niejednorodna/nierównomierna.