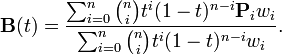Krzywa Béziera
Aby zrozumieć jak funkcjonują krzywe i powierzchnie NURBS, musimy najpierw zapoznać się z krzywymi Béziera.
Są one krzywymi parametrycznymi, co oznacza, że każdy punkt należący do krzywej definiowany jest pewną funkcją liczby rzeczywistej będącej wspomnianym parametrem.
Krzywe Béziera dzielą się na krzywe wielomianowe i krzywe wymierne. Każda krzywa jest definiowana za pomocą łamanej kontrolnej, składającej się z punktów kontrolnych.
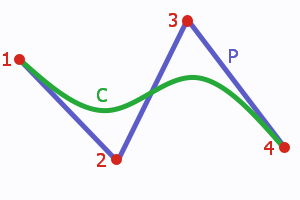
Następujący obrazek ukazuje przykładową krzywą Béziera (C), jej punkty kontrolne (1),(2),(3),(4), oraz jej łamaną kontrolna (P).
Krzywe wielomianowe
Krzywa Béziera definiowana jest za pomocą zestawu n + 1 punktów kontrolnych P0, P1, ..., Pn.Kształ krzywej jest opisywany przez wielomiany, których stopień zależy od ilości punktów kontrolnych.
Przyjęło się stosowanie wielomianów Bernsteina, jako że punkty kontrolne są ich naturalnymi współczynnikami dzięki czemu nie trzeba wykonywać dodatkowych obliczeń.
Pierwszy i ostatni punkt zawsze znakują początek i koniec krzywej, natomiast punkty środkowe (jeśli istnieją) zazwyczaj nie leżą na krzywej.
Liniowe krzywe Béziera
Mając punkty P0 oraz P1, linowa krzywa Béziera jest odcinkiem pomiędzy nimi. Krzywa podana jest wzorem:B(t) = P0 + t(P1 - P0) = (1 - t)P0 + tP1 , t ∈ [0,1]
i odpowiada interpolacji liniowej.
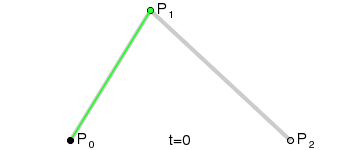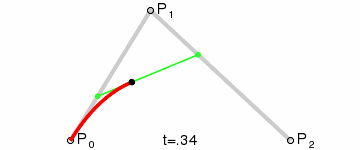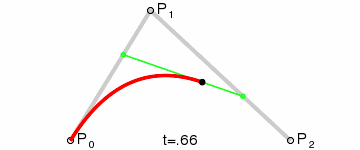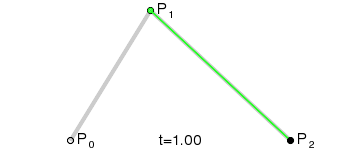
Kwadratowe krzywe Béziera
Kwadratową krzywą Béziera otrzymamy kreśląc funkcję B(t), mając punkty P0 ,P1 oraz P2.B(t) = (1 - t)[(1 - t)P0 + tP1] + t[(1 - t)P1 + tP2] , t ∈ [0,1]
może być interpretowane jako interpolacja liniowa odpowiadających punktów na krzywej liniowej z P0 do P1 oraz z P1 do P2. Upraszczając wyrażenie otrzymamy:
B(t) = (1 -t)2P0 + 2(1 - t)tP1 + t2P2 , t ∈ [0,1]
Sześcienne krzywe Béziera
Cztery punkty P0 ,P1 ,P2 oraz P3 definiują sześcienną krzywą Béziera.Może być ona określona jako liniowe połączenie dwóch kwadratowych krzywych Béziera, gdzie BPi,Pj,Pk(t) oznacza kwadratową krzywą Béziera zdefiniowaną przez punkty Pi,Pj,Pk:
B(t) = (1 - t)BP0,P1,P2(t) + BP1,P2,P3(t) , t ∈ [0,1]
Uproszczona wersja funkcji to:
B(t) = (1 -t)3P0 + 3(1 - t)2tP1 + 3(1 - t)t2P2 + t3P3 , t ∈ [0,1]
Narysuj własną sześcienną krzywą Béziera ustawiając punkty kontrolne kliknięciami myszy.
Krzywe Béziera o większej ilości punktów kontrolnych
Wzór na krzywą Béziera o większej niż 4 ilości punktów kontrolnych można zapisać jako: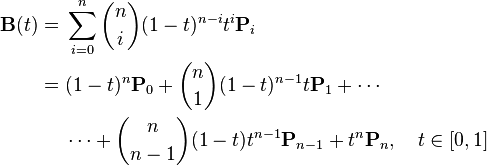
Gdzie:
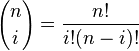
Narysuj własną krzywą Béziera o nieograniczonej ilości punktów kontrolnych ustawiając punkty kontrolne kliknięciami myszy.
Krzywe wymierne
Wymierne krzywe Béziera wprowadzają dające się regulować wartości wagowe punktów kontrolnych dla bardziej precyzyjnego manipulowania krzywą.Każdy punkt kontrolny ma przypisaną wagę, która określa jak bardzo punkt "przyciąga" krzywą do siebie.
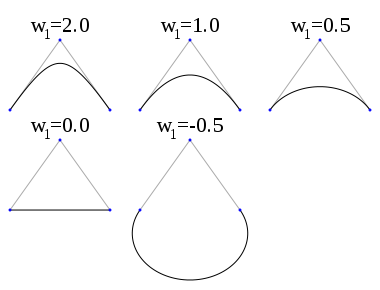
Mając zestaw n + 1 punktów kontrolnych Pi, wymierną krzywą Béziera można opisać jako:
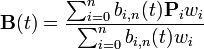
Po uproszczeniu wzór wygląda następująco: