Fascynacja trójkatem

Strona główna | Trójkąt | Twierdzenie Pitagorasa | Twierdzenie Talesa | Twierdzenie Feuerbacha | Okrąg 9 punktów | Okręgi dopisane | Prosta Eulera | Ci sławni | Zadania | Kontakt

Okrąg dziewięciu punktów

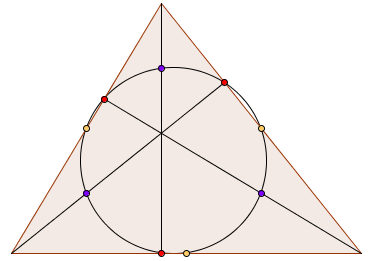
Co to takiego jest ten okrąg dziewięciu punktów (nazywany też okręgiem Feuerbacha lub Eulera) i jaki ma związek z trójkątem? Otóż, przechodzi on przez następujące punkty:

• środki boków trójkąta,
• spodki wysokości trójkąta,
• środki odcinków, łączących wierzchołki trójkąta z jego ortocentrum.

Ale czy tak jest na pewno? Spróbujmy to udowodnić.

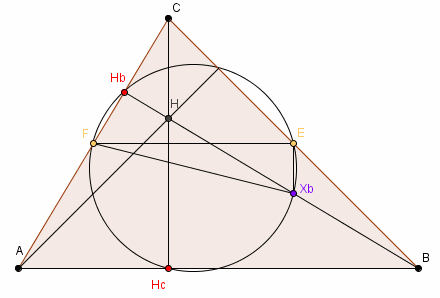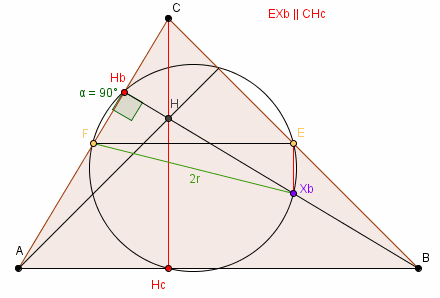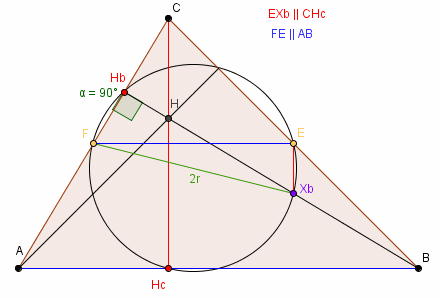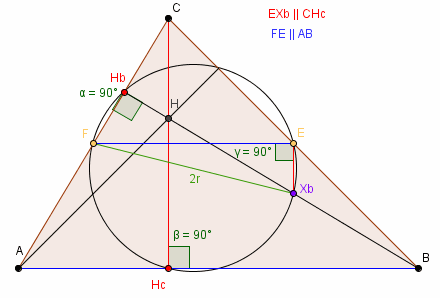
Dowód

Odcinek FX_b jest średnicą okręgu opisanego na ΔFX_bH_b, ponieważ ∠BH_bF jest kątem prostym.
Ponieważ punkt E jest środkiem BC, a X_b jest środkiem BH:
BE : BC = BX_b : BH = 1 : 2, z twierdzenia odwrotnego do twierdzenia Talesa ⇒ X_bE || H_cC.
CF : CA = CE : CB = 1 : 2 ⇒ FE || AB.
∠X_bEF = ∠CH_cB = ∠BH_bF = 90° ⇒ X_b, E, F, H_b leżą na jednym okręgu.

W analogiczny sposób otrzymujemy, że na tym okręgu leżą punkty D oraz X_c, H_c i X_a, H_a.

Czy okrąg 9 punktów musi mieć 9 punktów?

Co będzie w przypadku, gdy stworzymy trójkąt prostokątny?

Jak widać niektóre punkty pokryły się i w rezultacie otrzymaliśmy tylko 5 punktów. Wyżej przedstawiony jest trójkąt nierównoramienny. A co by się stało, gdyby ten trójkąt miał dwa ramiona równej długości?

Teraz nasz okrąg ma 4 punkty z 9. Sprawdźmy, co stanie się dla trójkąta równoramiennego i równobocznego.

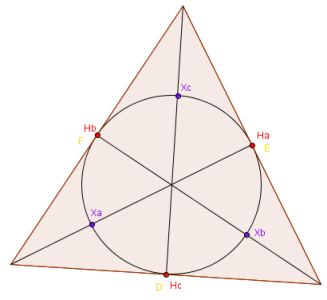
Widzimy, że w przypadku trójkąta równoramiennego i równobocznego otrzymujemy odpowiednio 8 i 6 punktów. W trójkącie rozwartokątnym również może się zdarzyć, że w zależności od rozwartości kątów, niektóre z 9 punktów pokryją się, jak na przykład tutaj:

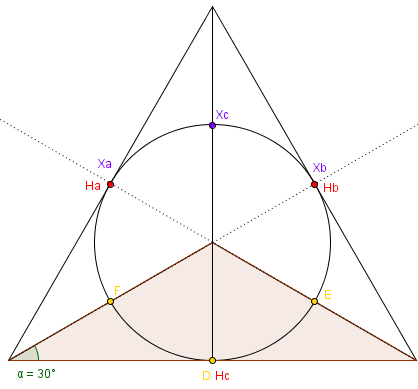
Gdzie jest środek?

Wiemy przez jakie punkty przechodzi okrąg 9 punktów, ale nie wiemy jeszcze, gdzie jest jego środek. Znajdziemy go na prostej Eulera.
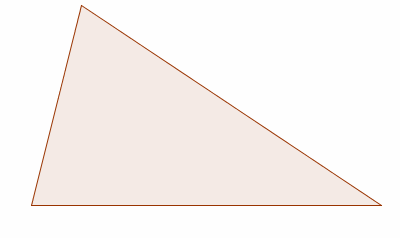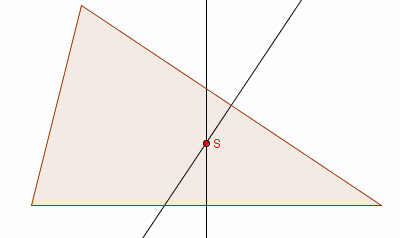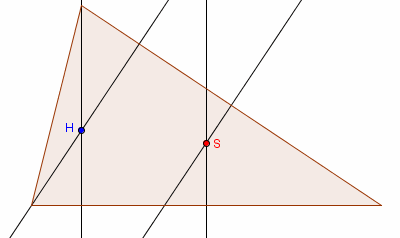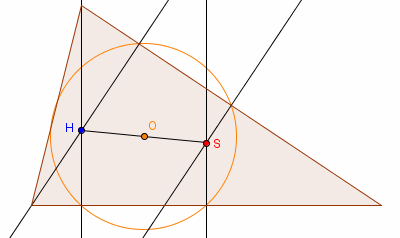
Środek tego okręgu, jest środkiem odcinka łączącego ortocentrum trójkąta (punkt przecięcia wysokości) ze środkiem okręgu opisanego na tym trójkącie (punkt przecięcia symetralnych).

Jak długi jest promień?

Połączmy punkt E ze środkiem okręgu 9 punktów. Prosta EO₉ przecina wysokość AK
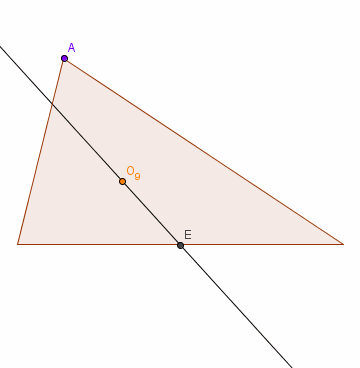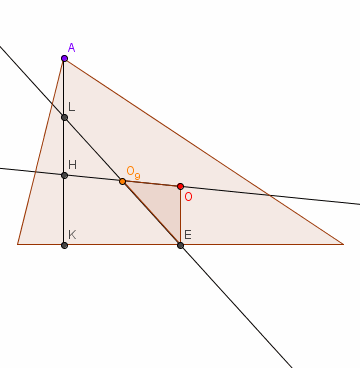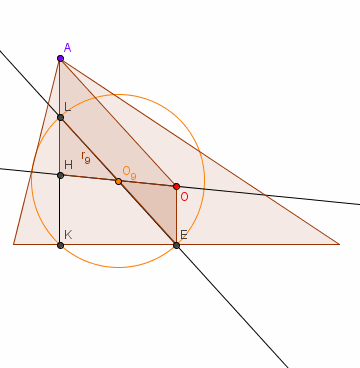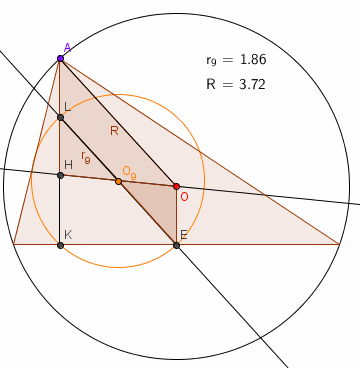
w punkcie L. LE jest średnicą okręgu 9 punktów. ΔO₉EO jest przystający do ΔO₉LH ⇒ OE = LH.
LH = AL, więc OE = AL. Czworokąt ALEO jest równoległobokiem i AO = LE, gdzie LE jest średnicą okręgu 9 punktów, a AO promieniem okręgu opisanego na trójkącie, czyli 2 r₉= R.