Fascynacja trójkatem
Prosta Eulera
Najpierw dowiedzmy się, czym jest ta prosta. Zachęcam też do
poczytania informacji o trójkącie.
Prosta Eulera dla trójkąta niebędącego trójkątem równobocznym jest to prosta, która przechodzi przez ortocentrum tego trójkąta, środek okręgu opisanego, środek ciężkości trójkąta oraz środek okręgu dziewięciu punktów.
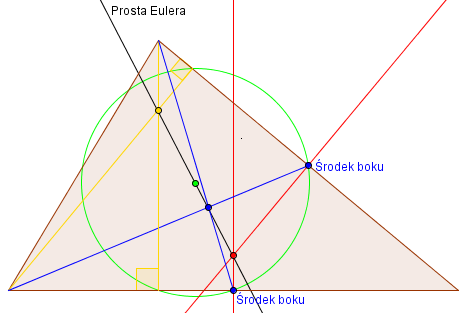
Czy faktycznie te punkty leżą na tej samej prostej?
Przedstawię prosty dowód na istnienie takiej prostej.
Oznaczmy kolejno punkty:
- A, B, C - wierzchołki trójkąta
- H - ortocentrum
- O - środek okręgu opisanego
- D - środek ciężkości
- E - środek okręgu dziewięciu punktów
Wtedy 2 B'H' = BH.
Czworokąt A'OB'H' jest równoległobokiem: OA' = B'H', czyli 2 OA' = BH.
Środek ciężkości D dzeli środkową BA' w stosunku 2:1, więc BD = 2 DA'
OA'||BH czyli ∠OA'D=∠HBD, bo są one kątami naprzemianległymi
ΔA'OD to obraz ΔHBD w jednokładności o środku D i skali 1:2 ⇒ punkty H, D, O leżą na tej samej prostej.
Środek okręgu dziewięciu punktów E, jest środkiem odcinka łączącego ortocentrum trójkąta ze środkiem okręgu opisanego na tym trójkącie, a więc też znajduje się na tej prostej.
