Trójkąt jaki jest, każdy widzi
Prawie wszyscy wiedzą, co to jest trójkąt i jak wygląda. Mimo to, spróbuję przedstawić parę podstawowych faktów i własności trójkąta.
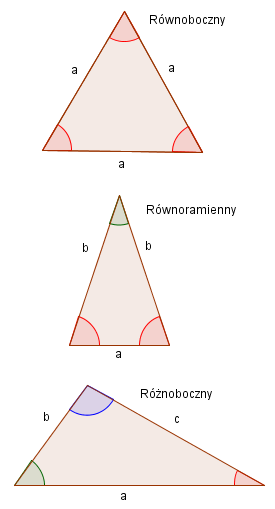
Trójkąt jest wielokątem o trzech bokach. Ze względu na długości boków możemy wyróżnić trójkąt:
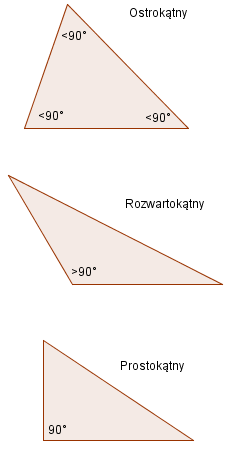
Ze względu na rozwartości trójkątów możemy wyróżnić trójkąt:
Suma miar kątów
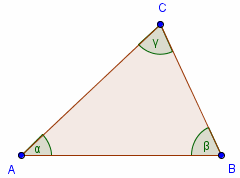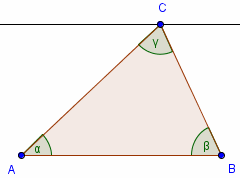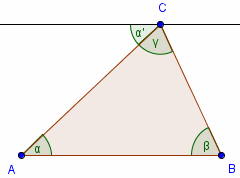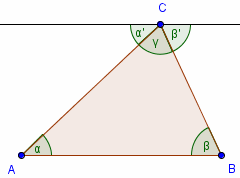
Suma miar kątów wewnętrznych trójkąta jest równa 180°. Skąd to wiadomo?
Rysujemy prostą równoległą do boku AB, która przechodzi przez wierzchołek
C. Kąty α i α' są równe, bo są kątami naprzemianległymi, podobnie
jak β i β'.
Z tego wynika, że α' + γ + β' =
180° = α + γ + β.
Kiedy można zbudować trójkąt?
Mówi nam o tym nierówność trójkąta: z odcinków a, b, c można zbudować trójkąt tylko wtedy, gdy: a + b > c, gdzie c jest długością najdłuższego boku.
Elementy trójkąta
Przedstawię jeszcze kilka ważnych elementów w trójkącie.
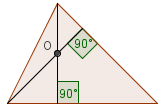
Wysokość to najkrótszy odcinek łączący jeden z wierzchołków trójkąta z prostą zawierającą przeciwległy bok trójkąta. Wysokości przecinają się w punkcie zwanym ortocentrum.
Środkowa trójkąta to odcinek łączący wierzchołek trójkąta ze środkiem przeciwległego boku. Środkowe przecinają się w punkcie zwanym środkiem ciężkości tego trójkąta.

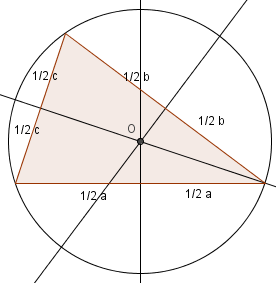
Symetralna boku trójkąta to prosta prostopadła do tego boku i przechodząca przez jego środek. Symetralne przecinają się w punkcie będącym środkiem okręgu opisanego na tym trójkącie.
Dwusieczna kąta to półprosta, o początku w wierzchołku kąta, która dzieli ten kąt na dwa kąty przystające. Dwusieczne przecinają się w punkcie będącym środkiem okręgu wpisanego w ten trójkąt.